Математическая статистика изучает массовые явления. В основе ее лежат предельные теоремы теории вероятностей. Эти теоремы рассматривают связь между теоретическими и экспериментальными характеристиками случайных величин, когда проводится большое число испытаний. «Законом больших чисел» называется группа теорем, которая доказывает, что в этом случае среднее значение перестает быть случайным результатом и может быть предсказано с достаточной точностью. «Центральная предельная теорема», названная так в силу особой важности, определяет условия, при которых закон распределения суммы случайных величин приближается к нормальному.
Неравенство Чебышева
Приведем рассуждение, впервые проведенное в XIX веке Чебышевым. Для чего запишем дисперсию случайной величины
.
Пусть a – любое положительное число. Оставим в написанной сумме только те члены, для которых 
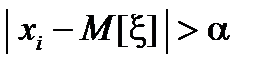, одновременно заменив множители 
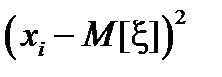на меньшую величину 
. Получим неравенство
.
Правая часть неравенства представляет собой сумму вероятностей тех значений xi, которые отстоят от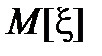 
в ту или другую сторону больше, чем на a. А вся сумма (по правилу сложения вероятностей) есть вероятность того, что величина 
получит какое-либо одно из этих значений. Это фактически означает, что полученное отклонение окажется больше, чем 
. Таким образом
.
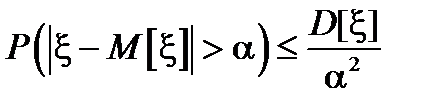Это неравенство Чебышева позволяет рассчитать вероятность отклонений случайной величины от ее среднего значения (в ту или другую сторону) больших, чем любое заданное число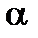 
. Такая оценка, хотя и грубая, может быть использована практически.
Например, используя неравенство, можно оценить вероятность того, что отклонение случайной величины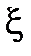 
от своего математического ожидания будет меньше 
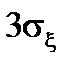, т.е. меньше трех среднеквадратических отклонений (правило трех сигм). Действительно, так как 
, то, записав неравенство Чебышева в несколько иной форме, получим
.
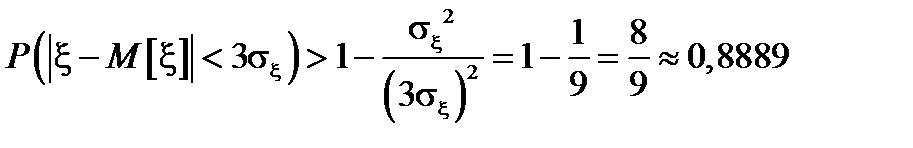Пример 26. Проводится 900 независимых испытаний некоторого события, вероятность наступления которого в каждом испытании равно 0,3. Оценить вероятность того, что число появлений этого события находится в пределах от 240 до 300. Использовать неравенство Чебышева.
Решение.
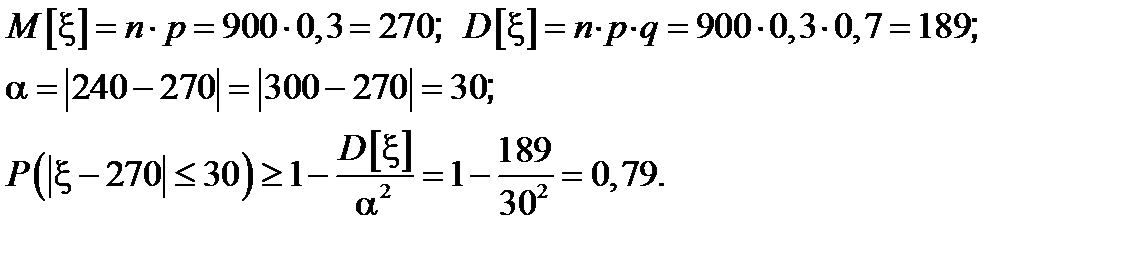
Теорема Чебышева
Эта теорема относится к фундаментальным результатам теории вероятностей и содержит основное утверждение закона больших чисел. Закон открыт великим русским математиком в середине XIX века.
Предположим, проведено большое количество независимых одинаковых испытаний, в каждом из которых наблюдается случайная величина одной и той же природы. С точки зрения математики наблюдается последовательность независимых случайных величин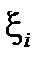 
. Тогда при условии существования такого числа С >0, что 
, для любого 
будет выполняться сходимость по вероятности.
Заметим, что случайные величины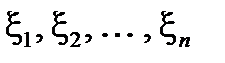 
можно рассматривать не только как значения наблюдаемой величины x в соответствующих независимых испытаниях, но и как независимые случайные величины, имеющие одинаковое распределение и такое же как у x. Применяя обратное неравенство Чебышева к среднему 
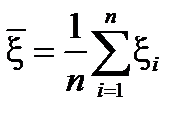, будем иметь
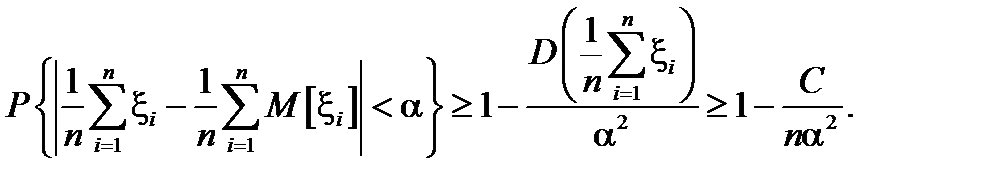(5)
Переходя к пределу при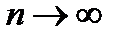 
, получим закон больших чисел в форме П.Л. Чебышева:
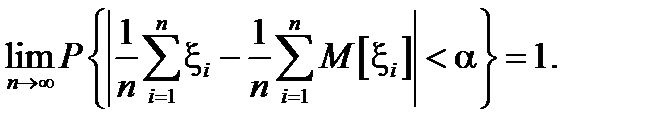
Если случайные величины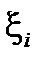 
имеют одинаковое распределение, то их математические ожидания и дисперсии одинаковы: 
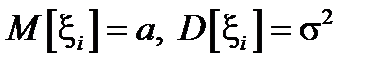, и в этом частном случае
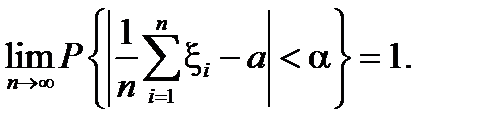
То есть, среднее арифметическое всех значений случайных величин 
, полученных в результате достаточно большого числа испытаний, с вероятностью, сколь угодно близкой к единице, приближается к неслучайному числу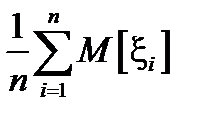 
(в частном случае равном a). Другими словами, разброс среднего арифметического по абсолютной величине сколь угодно мал.
Таким образом, как отдельная случайная величина может принимать значения, далекие от ее среднего значения (иметь значительное рассеяние), среднее арифметическое большого числа случайных величин ведет себя совершенно иначе, так как с подавляющей вероятностью принимает лишь значения, очень близкие к ее среднему (мало рассеяна). Объясняется это тем, что отклонения случайных величин в ту и в другую стороны при взятии среднего арифметического взаимно уничтожаются и суммарное отклонение оказывается малым в большинстве случаев.
Практическое применение теоремы Чебышева состоит в том, что о качестве большого количества однородного материала можно судить по сравнительно небольшой пробе (выборке). Суждения, сделанные по выборке, обладают большой точностью. Так, по небольшому объему зерна (в сравнении со всей партией) согласно закону больших чисел можно достаточно точно судить о среднем весе одного зерна и, следовательно, о качестве всей партии зерна.
Пример 27. Для случайной величины X известна дисперсия 
. Математическое ожидание (a) неизвестно. Полученное в 100 независимых испытаниях среднее значение этой случайной величины (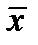
), принимают за ее математическое ожидание. Определить с вероятностью не менее 0,8 допускаемую при этом максимальную ошибку.
Решение. В задаче требуется найти ошибку ε из неравенства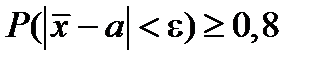 
. Используя формулу (5), получим 
Учитывая, что n =100, найдем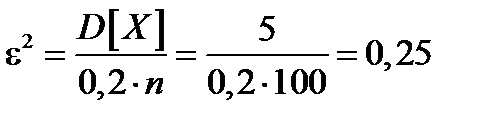 
и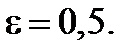 
Центральная предельная теорема
Это второе важнейшее положение теории вероятностей, называемое также теоремой Ляпунова. Выдающийся русский математик объяснил, почему на практике чаще всего встречаются нормально распределенные величины. Дело в том, что явления, исход которых зависит от случая, подвержены воздействию огромного количества случайных величин. Если эти действия выражаются случайными величинами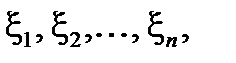 
то их суммарное влияние на явление можно выразить суммой 
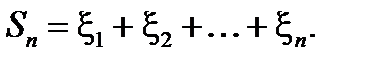Теорема утверждает, что если действующие причины взаимно независимы, их число очень велико и каждая из них ничтожно мало влияет на явление по сравнению с суммарным их действием, то закон распределения суммы в 
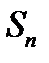лишь незначительно может отличаться от нормального закона распределения.
Практическое значение теоремы обусловлено тем, что многие случайные величины (такие как ошибки различных измерений, валютные курсы, объемы прибыли от реализации однородного товара и другие) можно рассматривать как сумму отдельных независимых слагаемых. Например, рассеяние снарядов при стрельбе из орудия будет подчиняться нормальному закону, поскольку является результатом воздействия огромного числа факторов: ничтожные изменения в состояниях атмосферы, колебания количества взрывчатого вещества и в форме различных снарядов, незаметные для глаза ошибки в наводке орудия и многие другие. Эти факторы независимы и влияние каждого на траекторию заряда ничтожно мало.
На практике (ситуация характерна для математической статистики) чаще всего используется частный случай теоремы, когда члены суммы 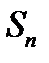имеют одинаковое распределение 
Тогда функция распределения центрированной и нормированной суммы этих величин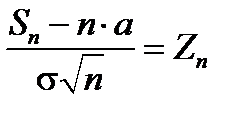 
стремиться при 
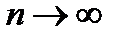к функции распределения стандартной нормальной случайной величины
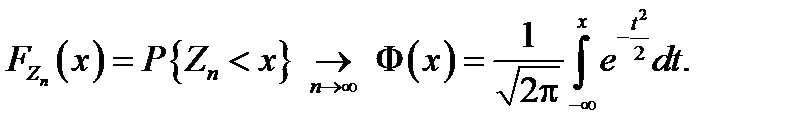
Это означает, что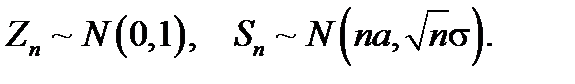 
Следствием центральной предельной теоремы являются локальная и интегральная теоремы Муавра-Лапласа.
