Биномиальный закон
Рассмотрим в качестве случайной величины X число наступлений некоторого события в n независимых испытаниях. Случайная величина X будет распределена по биномиальному закону с параметрами n и p, если она принимает значения 0, 1, 2, …, m, …, n, с соответствующими вероятностями:
где 
Вероятность каждого значения вычисляется по формуле Бернулли. Согласно этой формуде можно записать функцию распределения:
Среднее значение биномиального распределения и дисперсия принимают вид:
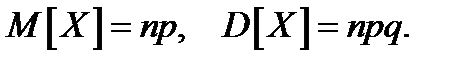
Пример 17. Торговый агент встретился с тремя потенциальными покупателями. Из опыта известно, что вероятность покупки равна 0,3. Какова вероятность того, что покупку совершит один покупатель, двое, все трое или ни один из них?
Решение. Задача подходит под условия биномитального эксперимента,так как: три испытания идентичны, независимы, и каждое испытание имеет лишь два исхода (успех-неуспех). По формуле Бернулли рассчитаем вероятности биномиального распределения:
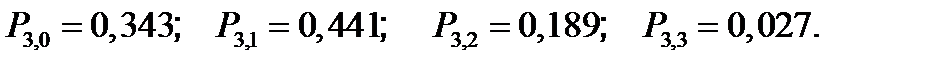
Математическое ожидание
,
или
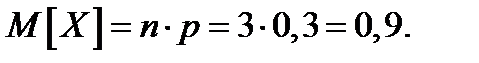
и дисперсия
Распределение Пуассона
Это предельное распределение биномиального закона, когда n велико 
и p мало 
, то есть закон распределения вероятностей массовых и редких событий.
Случайная величина X имеет распределение Пуассона с параметром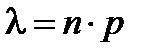 
, если ее возможные значения 0, 1, 2,…, а соответствующие вероятности вычисляются по формуле Пуассона
Существуют специальные таблицы распределения Пуассона. Математическое ожидание и дисперсия совпадают и равны параметру λ, который определяет этот закон:
Этот параметр характеризует среднюю интенсивность, с которой случайные события появляются независимо друг от друга.
Часто случайные события, происшедшие за фиксированный промежуток времени или в фиксированной области пространства подчиняются пуассоновскому распределению. Ими могут быть число поступивших вызовов на телефонную станцию за время t, число частиц радиоактивного распада, зарегистрированных счетчиком в течение некоторого времени t, число опечаток в большом тексте и т.д.
Пример 18. Прибытие машин на автостоянку может быть описано распределением Пуассона, если предположить, что вероятность прибытия в любые два равных промежутка времени одинакова и эти события независимы.
Решение. Пусть среднее число прибывающих машин за час равно 10. Тогда λ=10 и
для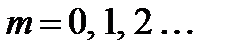 
Чтобы узнать вероятность прибытия в течение часа, например, пяти машин (m =5) достаточно рассчитать
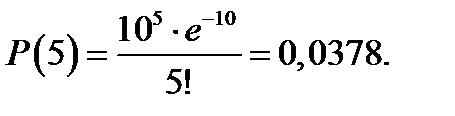
Геометрическое распределение
Дискретная случайная величина X будет распределена по геометрическому закону, если ее возможные значения m =1, 2, 3, 4, …, а вероятности этих значений определяются формулой
Это распределение рассматривает обычный биномиальный эксперимент, только вместо вычисления числа успехов, случайная величина определяет число испытаний до первого успеха.
Математическое ожидание и дисперсия равны соответственно
Пример 19. Пусть 1% населения обладает, например, экстрасенсорными способностями. Сколько людей в среднем надо опросить, чтобы набрать 10 экстрасенсов?
Решение. Каждый опрос – независимое испытание с вероятностью p =0,01. Число опрошенных до встречи с первым экстросенсом – геометрическая случайная величина X, среднее значение которой оценивается математическим ожиданием 
Для того, чтобы встретить 10 экстросенсов, надо опросить в среднем в 10 раз больше людей (на основании свойства аддитивности математического ожидания).
Гипергеометрический закон распределения
По формулам Бернули и Пуассона вычисляют вероятности появления события ровно m раз в n независимых повторных испытаниях. Если эти повторные испытания зависимы (осуществляются без возвращения и, следовательно, схема Бернулли не применима), то вероятность появления интересующего нас события m раз в n испытаниях определяется по формуле
где 
Параметры распределения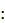 
N, M, n.
Математическое ожидание и дисперсия дискретной случайной величины X равны соответственно:
Событие, вероятность которого мы хотим определить, состоит, например, в следующем.
В лотерее разыгрывается N билетов, из которых M – выигрышные. Некто приобрел n билетов. Найти вероятность того, что из них m – выигрышные. Случайная величина X – число выигрышных билетов.
Пример 20. В торговый салон поступают партии машин по 10 штук. Обычно 2 из 10 машин не отвечают стандарту качества. Для контроля выбирают всегда 5 машин. Чему равна вероятность того, что хотя бы две машины из проверяемых будут забракованы?
Решение. Случайная величина X – число забракованных машин, принимает значение 2. Вероятность этого значения при N =10, M =2, N – M =8, n =5, m =2 будет
