вероятностей(вероятность произведения событий)
Рассмотрим задачу. Студент перед экзаменом выучил из 30 билетов билеты с номерами с 1 по 5 и с 26 по 30. Известно, что студент на экзамене вытащил билет с номером, не превышающим 20. Какова вероятность, что студент вытащил выученный билет?
Определим пространство элементарных исходов: W=(1,2,3,...,28,29,30). Пусть событие А заключается в том, чтостудент вытащил выученный билет: А = (1,...,5,25,...,30), а событие В – в том, что студент вытащил билет из первых двадцати: В = (1,2,3,...,20). Событие А ∩ В состоит из пяти исходов: (1,2,3,4,5), и его вероятность равна 5/30. Это число можно представить как произведение дробей 5/20 и 20/30. Число 20/30 – это вероятность события B. Число 5/20 можно рассматривать как вероятность события А при условии, что событие В произошло (обозначим её Р (А / В)). Таким образом, решение задачи определяется формулой
P (А ∩ В)= Р (B)× Р (А / В),
которая называется формулой умножения вероятностей, а вероятность Р (А / В) – условной вероятностью события A.
В другом способе записи эта формула имеет вид
P (А×В)= Р (B)× Р (А / В)= Р (A)× Р (B / A).
Тем самым вопрос о вычислении условной вероятности Р (А / В) сводится к вычислению двух безусловных вероятностей P (А×В) и Р (B), определенных на заданном вероятностном пространстве.
Вероятность произведения n событий A 1, A 2,…, An равна произведению одного из них на условную вероятность другого при условии, что первое произошло, на условную вероятность третьего при условии, что и первое и второе произошло и т.д.
Событие А называется независимым от события В (иначе: события А и В называются независимыми), если Р (А / В)= Р (А).
За определение независимых событий можно принять следствие последнего равенства и формулы умножения:
P (А ∩ В)= Р (А)× Р (B),
или
P (АВ)= Р (А)× Р (B).
Если события A 1, A 2,…, An попарно независимы, то вероятность наступления хотя бы одного из них проще вычисляется не по формуле сложения, а по формуле умножения вероятностей:
.
Пример 11. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями 0.851, 0.751, и 0.701. Найти вероятность того, что за время Т выйдет из строя:
а) только один элемент;
б) хотя бы один элемент.
Решение. Испытание, т.е. работу за время Т, нужно рассмотреть на двух уровнях: на уровне устройства и на уровне элементов. Вероятности элементарных событий заданы.
а) Обозначим за А 1 событие, когда за время Т выходит из строя только один элемент;
В 1 – первый элемент выходит из строя;
В 2 – второй элемент выходит из строя;
В 3 – третий элемент выходит из строя;
– первый элемент не выходит из строя;
– второй элемент не выходит из строя;
– третий элемент не выходит из строя;
Учитывая независимость элементов устройства, а также несовместность событий 
и 
, получаем следующую формулу:
По условию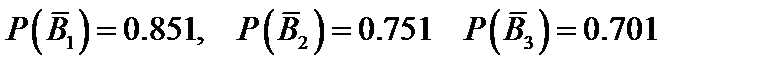 
,
следовательно 
.
Таким образом,
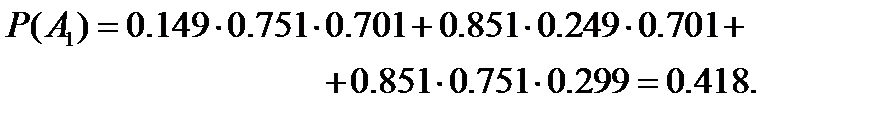
б) А 2 – событие, когда за время Т выходит из строя хотя бы один элемент; событие определяется словами “хотя бы”, значит, используем противоположное событие 
– за время Т все элементы работают безотказно.
Пример 12. В кармане лежит n ключей, из которых только один подходит к замку. Ключи по одному достают из кармана. Какова вероятность того, что нужный ключ будет вынут при k -м извлечении?
Решение. Обозначим через Ak событие, состоящее в том, что нужный ключ вынули на k -м шаге, соответственно 
состоит в том, что на этом шаге достали не тот ключ. Событие, вероятность которого требуется найти, есть произведение 
(первые k –1 раз достали не тот ключ, а на k -й раз вынули нужный).
Очевидно, что
,
т.е. (n –1) ненужных из n ключей;
,
если в первый раз достали неправильный ключ, в кармане осталось (n –1) ключей, из них (n –2) не подходят;
и так далее:
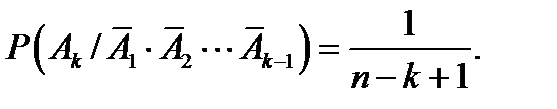
Если (k –1) раз доставали неправильный ключ, то в кармане осталось (n – k +1) ключей, из них один подходящий. Значит
Итак,
