Дифференциальные уравнения – это уравнения, связывающие неизвестную функцию и ее производные.
В самом общем виде дифференциальное уравнение записывается так 
.
Порядок старшей производной, входящей в состав уравнения, называется порядком уравнения.
Многие физические (и не только) уравнения имеют вид дифференциальных уравнений. Рассмотрим несколько примеров.
1. Уравнение механического движения: 
, где х = х (t) – неизвестная функция, m и F – известные величины. В зависимости от условий задачи получают различныедифференциальные уравнения:
а) сила постоянна. Уравнение движения примет вид
б) сила периодически изменяется со временем, например по закону 
. Уравнение движения 
в) сила пропорциональна смещению (движение идеально упругой пружины): 
. Уравнение движения:
г) сила, обратно пропорциональная квадрату расстояния,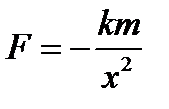 
(свободный полет). Уравнение движения: 
д) постоянная сила тяжести 
и сила трения 
, пропорциональная скорости, действующие одновременно (падение с трением). Уравнение движения:
.
Все приведенные уравнения – дифференциальные уравнения второго порядка.
2. Радиоактивный распад. Экспериментальные данные показывают, что скорость изменения массы пропорциональна массе вещества в данный момент: 
.
3. Электрическая цепь. Если в цепи, состоящей из последовательно соединенных резистора R и конденсатора C, произошло короткое замыкание, то напряжение U на конденсаторе будет меняться по закону 
.
4. Народонаселение. Представим число жителей страны в момент времени t как функцию L = L (t). Допустим, что за единицу времени народонаселение увеличивается на определенный процент. Тогда за период времени 
появится новых жителей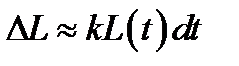 
. Для скорости роста L, таким образом, можно записать дифференциальное уравнение 
.
По такому же закону (закон естественного роста) размножаются и бактерии, и нейтроны в ядерных реакциях.
За триста лет существования дифференциального и интегрального исчислений появились многие тысячи дифференциальных уравнений. Однако замечательно то, что многие уравнения похожи друг на друга, например, последние три выше приведенные, т.е. совершенно разные процессы привели к одной и той же математической модели. В них скорость изменения искомой функции пропорциональна значению этой функции 
.
Процесс нахождения решений называется интегрированием дифференциального уравнения. Методы решения разнообразны и зависят от вида этих уравнений.
Общим решением дифференциального уравнения называется функция вида 
. Если постоянным 
придать конкретные числовые значения, то полученная функция будет называться частным решением.
Нахождение частного решения, удовлетворяющего начальному условию 
при 
, называется задачей Коши.
В том случае, когда уравнение не имеет элементарного решения, используют численные методы.
Решение уравнения 
(или 
) хорошо известно: 
, где С – произвольная постоянная. При различных значениях С получается семейство кривых, которые все удовлетворяют заданному уравнению. Если в дополнение к дифференциальному уравнению задать значение у для некоторого значения x, то можно определить постоянную С. Например, предположим, что решение должно проходить через точку х =0, у =1, то есть у (0)=1. Легко найти, что С =1 и что из всего семейства кривых только одна удовлетворяет одновременно и уравнению и условию.
Пример 8. Найти общее решение дифференциального уравнения с разделяющимися переменными 
Решение. Учитывая, что 
, перепишем уравнение в виде 
Разделим переменные: 
Проинтегрируем обе части уравнения: 
Общее решение будет иметь вид: 
