Вычислять вероятности P (w i) можно, используя априорный подход, который заключается в анализе специфических условий данного эксперимента (до проведения самого эксперимента). Классическое определение вероятностей основано на понятии равновозможных событий.
Два или несколько событий называются равновозможными, если условия их появления одинаковы и нет оснований считать, что какое-либо из них имеет больше шансов появиться в результате опыта, чем другое.
Возможна ситуация, когда пространство элементарных исходов состоит из конечного числа N элементарных исходов, причем случайный эксперимент таков, что вероятности осуществления каждого из этих N элементарных исходов представляются равными.
Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросание правильной игральной кости, случайное извлечение игральной карты из перетасованной колоды. В силу введенной аксиомы вероятности каждого элементарного исхода в этом случае равны  . Из этого следует, что если событие А содержит NA элементарных исходов, то
. Из этого следует, что если событие А содержит NA элементарных исходов, то
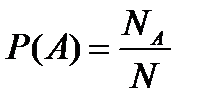 .
.
В данном классе ситуаций вероятность события определяется как отношение числа благоприятных исходов к общему числу всех несовместных равновозможных исходов.
Чтобы пользоваться этим классическим определением вероятности, нужно уметь подсчитывать общее число исходов эксперимента и число благоприятных исходов. Такой подсчет сводится к перебору вариантов. Раздел математики, в котором исследуются различные задачи на перебор, называется комбинаторикой.
Элементы комбинаторики
Пусть имеется множество Un, состоящее из n элементов.
Перестановкой из n элементов называется заданный порядок во множестве Un:
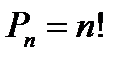
Размещением из n элементов по k элементов будет называться любое упорядоченное подмножество, состоящее из k элементов множества Un:
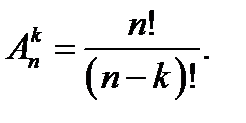
Сочетаниями из n элементов по k элементов называются подмножества, состоящее из k элементов множества Un. Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).

Пример 9. В соревнованиях принимают участие 16 команд. Сколькими способами могут распределиться три первых места?
Решение. Иными словами, необходимо найти число всех подмножеств, состоящих из трех элементов, отличающихся составом (номерами команд) или порядком их размещения. Таким образом, необходимо определить число размещений из 16 по 3:
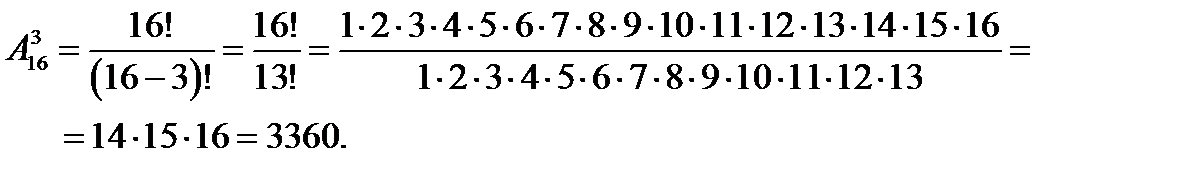
2.3 Статистическое определения вероятности.
Частота и вероятность
Рассмотрим случайный эксперимент, где нет симметрии, предопределяющей равновозможные исходы. Например, подбрасывается кубик, сделанный из неоднородного материала. Из физики известно, что кубик более часто будет падать на ту грань, которая ближе к центру тяжести. Как определить вероятность выпадения, например, трех очков? Вычислить вероятность, используя классическое определение, в этом случае нельзя. (Почему?) Наверное, чтобы проявилась вероятность, надо подбросить этот кубик n раз (где n – достаточно большое число, скажем n =1000 или n =5000), подсчитать число выпадений трех очков n 3 и считать вероятность исхода, заключающегося в выпадении трех очков, равной n 3/ n.
Это отношение называется относительной частотой или эмпирической вероятностью.
Аналогичным образом можно определить вероятности остальных элементарных исходов – единицы, двойки, четверки и т.д.
Если повторять серию бросаний, увеличивая n в каждой серии, то можно убедиться, что частота появления трех очков начнет колебаться возле одной определенной величины (вероятности события).
Говорят, что относительная частота стабилизируется около этого значения. Такое поведение характерно для любого случайного события и называется законом статистической устойчивости:
При неограниченном возрастании числа случайных экспериментов относительная частота каждого исхода имеет тенденцию к стабилизации.
Итак, случайное событие характеризуется тремя особенностями:
- неопределенностью исхода единичного эксперимента;
- возможностью неограниченного повторения в одинаковых условиях;
- стабилизацией относительной частоты.
Немецкий математик Р. Мизес предлагал определить вероятность Р (А) случайного события А через предел его эмпирической вероятности:
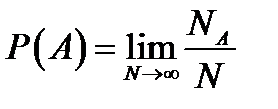 .
.
Однако, можно ли на практике выполнить бесконечно большое число однотипных испытаний? К тому же предел, строго говоря, не существует. Следовательно, частотное определение вероятности оказалось несостоятельным.
Уточнение понятия вероятности произошло на основе аксиоматического подхода, разработанного А.Н.Колмогоровым.






