Интегральные вычисления возникли из потребности создать общий метод нахождения площадей, объемов и центров тяжести. Способ вычисления площади уходит корнями в III в. до н.э., когда Архимед изобрел метод «исчерпывания». Этот метод через две тысячи лет преобразовался в метод интегрирования.
Пусть в некоторой области определены функции 
и 
. Пусть 
. Тогда 
называется производной функции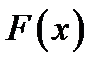 
, а 
– первообразной функции 
. Любая функция имеет множество первообразных.
По отношению к дифференцированию интегрирование является обратным действием.
Неопределенным интегралом от функции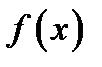 
называется ее произвольная первообразная
,
если 
, где х – переменная интегрирования, а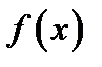 
– подынтегральная функция.
Геометрически неопределенный интеграл представляет семейство плоских кривых, смещенных друг относительно друга вдоль вертикальной оси.
Свойства неопределенного интеграла
1. Дифференциал неопределенного интеграла равен подынтегральному выражению
.
2. Неопределенный интеграл дифференциала функции равен самой функции с точностью до произвольной постоянной
.
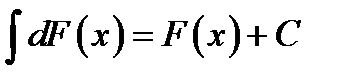3. Постоянная выносится из под знака интеграла
.
4. Интеграл суммы равен сумме интегралов
.
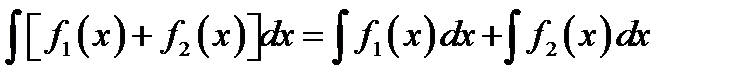5. Под знаком интеграла можно проводить замену переменной
.
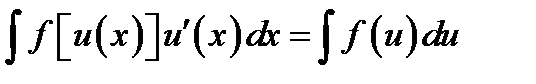Таблица основных интегралов получается из основных формул дифференциального исчисления путем прямого их обращения.
Так как интегрирование – действие обратное дифференцированию, то его можно проверить дифференцированием.
Всякое обратно действие сложнее прямого. Поэтому прежде чем воспользоваться таблицей интегралов приходится заданный интеграл преобразовывать к табличному. Наиболее часто используемые методы преобразования: метод разложения, метод подстановки (замена переменной), интегрирования по частям.
