Определенный интеграл отличается от неопределенного тем, что это либо число, либо первообразная с определенной постоянной.
Определенный интеграл 
можно представить как предел некоторой суммы
.
Здесь весь отрезок 
разбит на n отрезков 
, причем 
(или 
,или 
). Тогда 
– площадь прямоугольника.
Интуитивно ясно, что при 
интегральная сумма стремится к площади криволинейной трапеции.
Определенным интегралом от функции 
на отрезке 
называется предел интегральной суммы при стремлении максимального частичного отрезка разбиения к нулю.
Числа a и b носят название, соответственно, нижнего и верхнего пределов интегрирования.
Формула Ньютона-Лейбница
Определенный интеграл находится по формуле:
.
Свойства определенного интеграла:
1. 
.
2. 
.
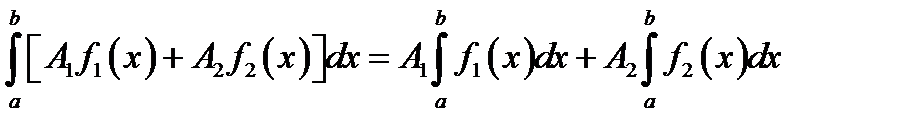3. 
.
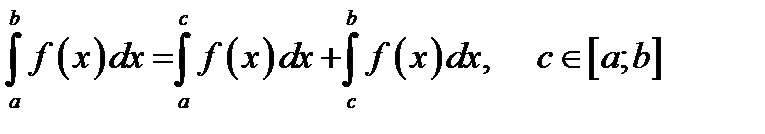4. 
.
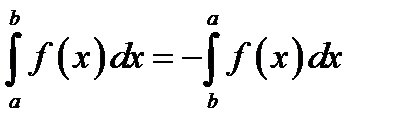5. 
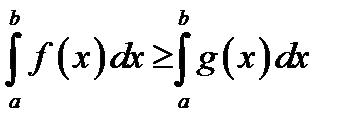, если 
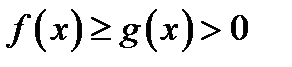на 
.
Геометрический смысл определенного интеграла: определенный интеграл 
равен площади криволинейной трапеции, ограниченной кривой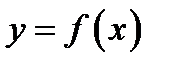 
и прямыми 
.
Механический смысл определенного интеграла: на графике ускорения отображает скорость, а на графике скорости отображает путь, пройденный телом при равноускоренном движении от t = 0 до момента t, если в начальный момент скорость и путь равны нулю.
Пример 7. Вычислить площадь, ограниченную параболами 
Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
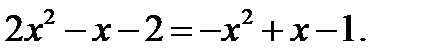
Решая квадратное уравнение, определим его корни: 
и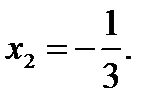 
Тогда искомая площадь будет равна:
