Пусть существует 
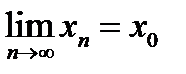и 
причем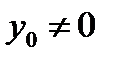 
тогда при 
Вопрос о существовании предела последовательности часто бывает сложным. Вычисление предела – это раскрытие неопределенности вида: 
и т.д. При этом используются так называемые замечательные пределы:
Непрерывность функции и ее пределы
Приращением функции называется изменение функции при заданном приращении аргумента:
.
Функция f (x) непрерывна в точке x 0, если она определена в этой точке и в некоторой ее окрестности и приращение функции в этой точке стремится к нулю при стремлении к нулю приращения аргумента: 
, если 
.
График непрерывной функции можно нарисовать, не отрывая пера от бумаги.
Точка, в которой при стремлении к нулю приращения аргумента приращение функции к нулю не стремится, называется точкой разрыва функции.
Будем считать, что функция f (x) определена во всех точках некоторого интервала, содержащего точку x 0 (т.е. в окрестности точки x 0), кроме, быть может, самой точки x 0.
Число A называется пределом функции y = f (x) при 
, если для произвольного (сколь угодно малого) положительного числа 
существует такое положительное число 
, зависящее от , что для всех точек х из -окрестности точки x 0, исключая, быть может, саму точку x 0 (т.е. для всех, удовлетворяющих неравенству 
), будет выполняться неравенство 
. Сказанное обозначают как 
.
Запишем определение предела с помощью кванторов:
Число А называют пределом функции f (x) на бесконечности (в бесконечно удаленной точке), если для 
найдется такое М >0, что при x > M выполняется неравенство 
и записывают: 
.
Для исследования поведения функции вблизи некоторых точек полезно знать, к чему стремится f (x), когда 
, оставаясь левее x 0 (т.е. при x < x 0), и когда 
, оставаясь правее x 0 (x > x 0). Такие пределы называются левым и правым пределом функции в точке x 0 или односторонними пределами. Обозначения: 
и 
.
Предел функции в точке x 0 существует, если предел справа равен пределу слева.
Функция y = f (x) с областью определения D называется непрерывной в точке x 0, если выполняются следующие три условия:
1. Функция y = f (x) определена в точке x 0, т.е. 
;
2. Существует предел функции в точке x 0;
3. Предел функции в этой точке равен значению функции в этой точке: 
.
Если в точке x 0нарушено хотя бы одно из трех приведенных условий, то точка x 0называется точкой разрыва функции y = f (x).
Функция f (x) имеет в точке x 0 разрыв первого рода, если пределы слева и справа конечны, но не равны друг другу.
Функция f (x) имеет в точке x 0 разрыв второго рода, если хотя бы один из пределов слева или справа бесконечен или не существует.
Если функция не определена в точке x 0или нарушено условие 
, то точка x 0называется точкой устранимого разрыва функции y = f (x).
Пример 5. Найти предел функции 
.
Решение. Вычислим пределы числителя и знаменателя:
Получили неопределенность типа 
. Для раскрытия неопределенности преобразуем дробь, разложив числитель и знаменатель на множители:
.
Разделим числитель и знаменатель дроби на (х –2). Это сокращение допустимо, так как при отыскании предела рассматриваются значения х ¹2 (это подчеркивается в определении предела). Тогда:
