Источником дифференциального исчисления были две проблемы:
1. О нахождении касательной к произвольной линии;
2. О нахождении скорости при произвольном законе движения.
Обе они привели к одной и той же вычислительной задаче. Она состоит в том, чтобы по данной функции f (x) отыскать другую функцию f ¢(x), представляющую скорость изменения функции f (x) относительно изменения аргумента. В таком общем виде задача была поставлена в XVII веке Ньютоном и Лейбницем. Они ввели символику, развили аппарат дифференциального исчисления и применили его к решению многих задач геометрии и механики.
Производной функции y = f (x) в точке x 0называется предел отношения приращения функции 
в этой точке к вызвавшему его приращению аргумента 
при произвольном стремлении 
к нулю.
Итак, по определению
.
Наряду с обозначением 
для производной употребляются и другие обозначения, например: y ¢, y ¢ x 
.
Производная имеет следующие механический и геометрический смыслы.
– скорость прямолинейного движения материальной точки в момент времени t 0 есть производная от пути по времени 
.
– угловой коэффициент касательной к графику функции в точке с абсциссой x 0равен значению производной этой функции в точке x 0: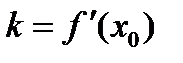 
.
Значит уравнение касательной к графику y = f (x) в точке 
имеет вид 
.
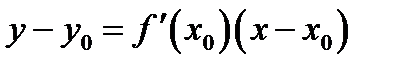Нормалью в точке 
к линии называется перпендикуляр к касательной в точке М 0. Ее уравнение имеет вид
,
так как угловой коэффициент нормали 
связан с угловым коэффициентом касательной 
условием перпендикулярности
.
Для одной и той же функции y = f (x) производную можно вычислять в различных точках.
Функция y = f (x), имеющая конечную производную в точке x 0, называется дифференцируемой в этой точке. Функция y = f (x) называется дифференцируемой в интервале 
, если она дифференцируема в каждой точке этого интервала.
Справедлива следующая теорема о связи между дифференцируемостью и непрерывностью.
Теорема: если функция y = f (x) дифференцируема в точке x 0, то она непрерывна в этой точке.
Обратная теорема неверна: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми, например функция 
.
Пример 6. Найти производную функции 
.
Решение. 
Производные высших порядков
Пустьфункция y = f (x) дифференцируема на интервале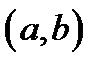 
. Тогда ее производная 
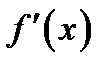является функцией от х. Пусть эта производная также имеет производную. Эта производная называется второй производной или производной второго порядка функции f (x). Она обозначается символом 
или 
.
Вообще, производной n-го порядка функции y = f (x) называется первая производная от производной (n –1) порядка
.
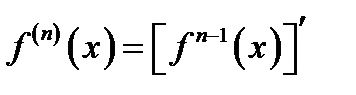Механический смысл второй производной: ускорение прямолинейного движения равно второй производной от пути по времени.
Правила Лопиталя. Понятие производной применимо для раскрытия неопределенностей типа 
или 
.
Правило 1. Пусть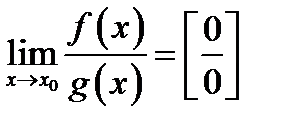 
, (или 
). Тогда, если существует предел отношения производных 
(или 
), то существует предел отношения функций, и эти пределы равны между собой, т.е.
(или 
).
Правило 2. Пусть 
(или 
).
Тогда, если существует предел отношения производных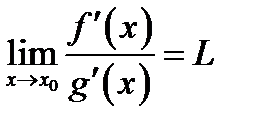 
(или 
), то существует предел отношения функций, и они равны между собой, т.е.
(или 
).
