Пусть имеем функцию y = f (x), определенную на промежутке D и непрерывную в точке 
. Тогда приращению аргумента 
отвечает приращение функции
,
бесконечно малое вместе с 
.
Большую важность имеет вопрос: существует ли для 
такая линейная однородная относительно 
бесконечно малая 
, что их разность оказывается, по сравнению с 
, бесконечно малой высшего порядка малости
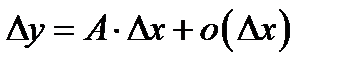, (1)
где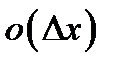 
есть величина, стремящаяся к нулю при 
быстрее, чем 
.
При 
равенство (1) показывает, что бесконечно малая 
(главная часть приращения 
) эквивалентна бесконечно малой 
. В этом случае выражение 
называется дифференциалом функции и обозначается символом 
или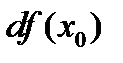 
.
Доказывается, что для того, что бы функция y = f (x) в точке 
имела дифференциал, необходимо и достаточно, чтобы она была дифференцируема в точке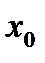 
(т.е. имела в этой точке конечную производную 
). При этом 
и формула (1) имеет вид 
.
Итак, дифференциал всегда равен 
.
Дифференциал аргумента 
. То есть приращение аргумента тождественно равно дифференциалу аргумента. Тогда производную функции можно выразить через дифференциалы функции и аргумента:
.
Геометрический смысл дифференциала: в то время как 
есть приращение ординаты кривой y = f (x), dy является приращением ординаты касательной.
В приложениях часто бывает более удобно работать с дифференциалом, чем с производной в точке. Кроме того, дифференциал – главная часть приращения функции и может быть вычислен сравнительно просто. Дифференциал является источником приближенных формул, так как при 
. Подробнее:
,
откуда
.
Например, надо найти приближенно 
. Легко вычисляются значения 
и 
при 
. Тогда
.
