Топология – раздел математики, который занимается изучением пределов и непрерывностью функций. В соединении с алгеброй топология составляет общую основу математики.
Топологическое пространство или фигура – подмножество нашего однородного евклидового пространства, между точками которого задано некоторое отношение близости. Здесь рассматриваются фигуры не как жесткие тела, а как объекты, сделанные как бы из очень эластичной резины, допускающие непрерывную деформацию, сохраняющую их качественные свойства.
Взаимно-однозначное непрерывное отображение фигур называется гомеоморфизмом. Другими словами, фигуры гомеоморфны, если одну можно перевести в другую непрерывной деформацией.
Примеры. Гомеоморфны следующие фигуры (из разных групп фигуры не гомеоморфны), изображенные на рис. 2.
Рис. 2.
1. Отрезок и кривая без самопересечений.
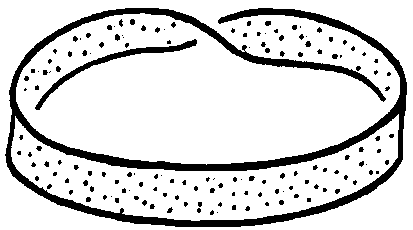
2. Круг, внутренность квадрата, лента.
3. Сфера, поверхность куба и тетраэдра.
4. Окружность, эллипс и заузленная окружность.
5. Кольцо на плоскости (круг с дыркой), кольцо в пространстве, два раза перекрученное кольцо, боковая поверхность цилиндра.
6. Лист Мёбиуса, т.е. один раз перекрученное кольцо, и три раза перекрученное кольцо.
7. Поверхность тора (бублика), сфера с ручкой и заузленный тор.
8. Сфера с двумя ручками и крендель с двумя дырками.
В математическом анализе функции изучаются методом пределов. Переменная и предел – основные понятия.
В различных явлениях некоторые величины сохраняют свое численное значение, другие изменяются. Совокупность всех числовых значений переменной величины называется областью изменения этой переменной.
Из разнообразных способов поведения переменной величины наиболее важен такой, при котором переменная величина стремится к некоторому пределу.
Постоянное число a называется пределом переменной величиныx, если абсолютная величина разности между x и a (
) становится в процессе изменения переменной величины x сколь угодно малой: 
Что значит «сколь угодно малой»? Переменная величина х стремится к пределу а,если для любого сколь угодно малого (произвольно малого) числа 
найдется такой момент в изменении переменной х,начиная с которого выполняется неравенство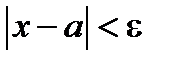 
.
Определение предела имеет простой геометрический смысл: неравенство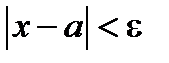 
означает, что х находится в 
-окрестности точки a, т.е. в интервале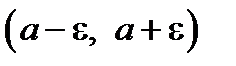 
.
Таким образом, определение предела можно дать в геометрической форме:
Число а является пределом переменной величины х, если для любой сколь угодно малой (произвольно малой) 
-окрестности числа а можно указать такой момент в изменении переменной х, начиная с которого все ее значения попадают в указанную -окрестность точки а.
Замечание. Переменная величина х может по-разному приближаться к своему пределу: оставаясь меньше этого предела (слева), больше (справа), колеблясь около значения предела.
Предел последовательности
Функцией называется закон (правило) по которому каждому элементу x некоторого множества X соответствует единственный элемент y множества Y.
Функция может быть задана на множестве всех натуральных чисел: 
. Такая функция называется функцией натурального аргумента или числовой последовательностью.
Так как последовательность, как и всякое бесконечное множество, нельзя задать перечислением, то она задается общим членом: 
, где 
– общий член последовательности.
Дискретной переменной называется общий член последовательности 
.
Для последовательности слова «начиная с некоторого момента» означают слова «начиная с некоторого номера».
Число а называется пределом последовательности 
, если для любого сколь угодно малого (произвольно малого) числа 
найдется такой номер N, что для всех членов последовательности с номером n > N выполняется неравенство 
.
или 
при 
.
Геометрически определение предела последовательности означает следующее: для любой сколь угодно малой (произвольно малой) 
-окрестности числа а найдется такой номер, что все члены последовательности с большими, чем N, номерами, попадают в эту окрестность. Вне окрестности оказывается лишь конечное число начальных членов последовательности. Натуральное число N зависит от : 
.
Запишем определение предела с помощью логических значков – кванторов:
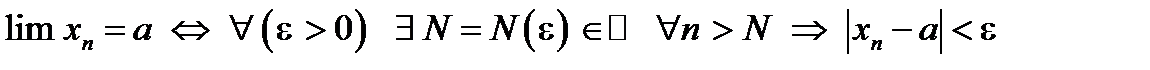при 
.
Последовательность называется бесконечно малой, если 
.
Последовательность называется бесконечно большо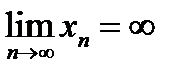й (
при 
), если для любого числа E >0 существует номер N (E) такой, что при n > N выполняется неравенство 
. Если при этом, начиная с некоторого номера, все члены последовательности положительны, то используют запись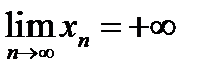 
.
Над последовательностями можно осуществлять обычные арифметические операции, и выполняют их почленно.
