Рассмотрим задачу (9.1.5)– (9.1.8) с измененными начальными условиями:

 , (9.2.1)
, (9.2.1)
 ,
,  ,
,  ,
, 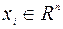 , (9.2.2)
, (9.2.2)
 ,
,  ,
, 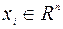 , (9.2.3)
, (9.2.3)
 ,
,  ,
,  , (9.2.4)
, (9.2.4)
где точка  и целое число
и целое число  фиксированы. Через
фиксированы. Через 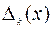 обозначим множество управлений
обозначим множество управлений 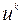 , удовлетворяющих (9.2.4) и таких, что соответствующая траектория
, удовлетворяющих (9.2.4) и таких, что соответствующая траектория  из (9.2.5) удовлетворяет фазовым ограничениям (9.2.3). Пару
из (9.2.5) удовлетворяет фазовым ограничениям (9.2.3). Пару  будем называть допустимой для задачи (9.2.1)–(9.2.4), если
будем называть допустимой для задачи (9.2.1)–(9.2.4), если  . Допустимую пару
. Допустимую пару  назовем решением задачи (9.2.1)–(9.2.4), если
назовем решением задачи (9.2.1)–(9.2.4), если

а  – оптимальным управлением,
– оптимальным управлением,  – оптимальной траекторией задачи (9.2.1)–(9.2.4).
– оптимальной траекторией задачи (9.2.1)–(9.2.4).
При  также и
также и  хотя бы для одного
хотя бы для одного  . Введем функцию
. Введем функцию

 ,
,
называемую функцией Беллмана задачи (9.1.5)-(9.1.8). Ее область определения – множество  . Функцией Беллмана задачи (9.1.5)-(9.1.8) удовлетворяет рекуррентным соотношениям, называемым уравнением Беллмана.
. Функцией Беллмана задачи (9.1.5)-(9.1.8) удовлетворяет рекуррентным соотношениям, называемым уравнением Беллмана.
Теорема 1. Функция Беллмана задачи (9.1.5)-(9.1.8) необходимо является решением уравнения

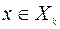 ,
,  , (9.2.5)
, (9.2.5)
где  ,
,
 ,
,  , (9.2.6)
, (9.2.6)
Верно и обратное: функция  ,
, 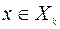 .
.  , определяемая условиями (9.2.5), (9.2.6), является функцией Беллмана задачи (9.1.5)-(9.1.8).
, определяемая условиями (9.2.5), (9.2.6), является функцией Беллмана задачи (9.1.5)-(9.1.8).






