Для функций многих переменных условие 
является достаточным условием минимума (максимума). Аналогичных условий для второй вариации 
(т.е. 
или 
) не хватает, чтобы получить достаточные условия экстремума для вариационной задачи. Для этого привлекают дополнительные условия, основанные на рассмотрении полей экстремалей. Мы будем рассматривать достаточные условия для слабого и сильного экстремумов для задачи Лагранжа (7.2.1) нахождения экстремума функционала
, 
, 
.
Будем говорить, что экстремаль 
можно расположить в поле экстремалей, если существует семейство экстремалей 
, где 
– параметр, такое, что
– оно покрывает определенную область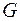 
плоскости 
так, что через каждую точку 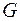проходит ровно одна экстремаль семейства;
– для данного 
получаем исходную экстремаль 
, причем она лежит не на границе области .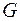
Поле экстремалей называется центральным, если все кривые поля исходят из точки 
(центр семейства экстремалей). Наклон проходящих через точку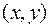 
экстремалей поля называется градиентом поля в точке 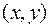и обозначается 
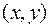; как функция от называется градиентной функцией.
Достаточным условием для включения экстремали в поле экстремалей (с центром 
является условие Якоби 
.
Определим Е – функцию Вейерштрасса
,
где 
- градиентная функция.
Достаточные условия экстремума:
а) Функция 
доставляет функционалу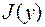 
слабый экстремум, если
1) является экстремалью, то есть удовлетворяет уравнению Э - Л и граничным условиям 
, ;
2) может быть включена в поле экстремалей;
3) знак функции 
не изменяется во всех точках 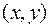, которые лежат достаточно близко от экстремали , и для всех значений 
, лежащих вблизи градиентной функции 
на экстремали. Функция 
доставляет функционалу минимум при 
и максимум при 
.
б) Функция доставляет функционалу 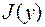сильный (локальный) экстремум, если
1) выполнены пп. 1) и 2) условий а);
2) функция не изменяет свой знак для всех точек 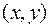, лежащих в достаточной близости от , и для любых значений 
. Функция у доставляет функционалу минимум при и максимум при .
Пример 7. Найти экстремум функционала
.
С учетом специального вида функции 
, имеем 
, и тем самым 
, т.е. экстремали являются прямыми вида 
. Отсюда, с учетом граничных условий найдем экстремаль 
.
Условие Лежандра выполнено в строгой форме:
.
Решение дифференциального уравнения Якоби (5.13)
имеет вид 
. Отсюда для сопряженной точки имеем 
. Следовательно, экстремаль удовлетворяет условиям Лагранжа и Якоби и может быть включена в поле экстремалей 
. Функция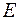 
имеет вид:
Первый сомножитель 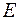- функции всегда неотрицателен, а второй положителен для значений , которые расположены около 1, то есть 
реализует слабый (локальный) минимум функционала. Условие сильного экстремума не выполнено, так как при 
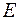- функция отрицательна.
Пример 8. Найти экстремум функционала
.
Экстремали этой задачи имеют вид
.
Применение граничных условий дает 
. Условия Лежандра и Якоби выполнены. Экстремаль 
может быть включена в поле 
.
Из соотношения 
видно, что для всех . Поэтому экстремаль реализует сильный (локальный) минимум.
