Задачей Лагранжа в ВИ называют задачу нахождения экстремума функционала (7.1.1) при условиях (7.1.2)
 ,
,  ,
,  . (7.2.1)
. (7.2.1)
Если нет специальных оговорок, то будем считать, что 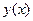 имеет непрерывную производную
имеет непрерывную производную 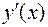 .
.
Необходимые условия экстремума. Уравнение Эйлера–Лагранжа (Э-Л). Если функция  доставляет функционалу
доставляет функционалу 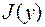 слабый (локальный) экстремум, то она должна являться решением дифференциального уравнения Эйлера-Лагранжа:
слабый (локальный) экстремум, то она должна являться решением дифференциального уравнения Эйлера-Лагранжа:
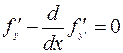 , (7.2.2)
, (7.2.2)
или в другой форме
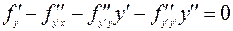 . (7.2.2)
. (7.2.2)
Здесь  предполагается дважды непрерывно дифференцируемой. Так как сильный (локальный) экстремум есть одновременно и слабый (локальный) экстремум, то дифференциальное уравнение (7.2.2) представляет собой так же и необходимое условие для сильного (локального) экстремума.
предполагается дважды непрерывно дифференцируемой. Так как сильный (локальный) экстремум есть одновременно и слабый (локальный) экстремум, то дифференциальное уравнение (7.2.2) представляет собой так же и необходимое условие для сильного (локального) экстремума.
Уравнение Эйлера-Лагранжа есть дифференциальное уравнение второго порядка. Решения этого уравнения называют экстремальными. Появляющиеся две постоянные интегрирования определяются при помощи граничных условий (7.1.2).
Краткое описание доказательства. Пусть  экстремум функционала (7.2.1). Для кривых сравнения вида
экстремум функционала (7.2.1). Для кривых сравнения вида
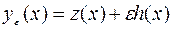 ,
, 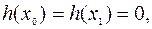 (7.2.3)
(7.2.3)
где 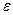 – малый параметр, имеем
– малый параметр, имеем
 .
.
Таким образом, функционал  есть функция только параметра
есть функция только параметра 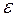 . В силу предположения о том, что
. В силу предположения о том, что  есть решение, должно выполнятся соотношение
есть решение, должно выполнятся соотношение
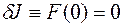 . (7.2.4)
. (7.2.4)
Вычислим производную 
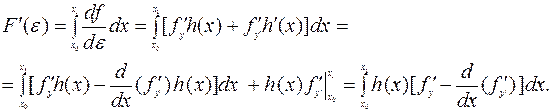
Из 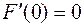 и произвольности функции
и произвольности функции 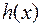 вытекает уравнение Эйлера – Лагранжа (7.2.2). В приведенном кратком обосновании используется факт существования решения.
вытекает уравнение Эйлера – Лагранжа (7.2.2). В приведенном кратком обосновании используется факт существования решения.
Пример 3. Найти экстремум функционала
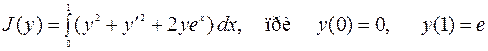 .
.
Уравнение Эйлера-Лагранжа имеет вид
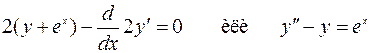 .
.
Отсюда следует 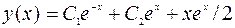 . Используя граничные условия, получаем:
. Используя граничные условия, получаем: 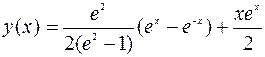 .
.
Следует учитывать, что экстремали не всегда реализуют минимум или максимум, так как уравнение Э-Л представляет собой только необходимое условие экстремума. Приведем дополнительные необходимые условия экстремума, которые в определенных случаях позволяют исключить те экстремали, которые не дают экстремума функционалу.
Специальные случаи задачи (7.2.1).
а) Если 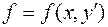 , т.е.
, т.е. 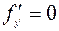 , то уравнение Э-Л имеет вид
, то уравнение Э-Л имеет вид 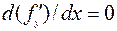 , так что
, так что  есть первый интеграл этого уравнения.
есть первый интеграл этого уравнения.
Пример 4. Найти экстремум функционала
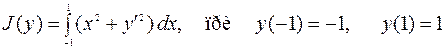 .
.
Из условия 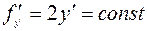 получаем, что
получаем, что 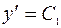 , и, следовательно,
, и, следовательно,  . Применяя граничные условия, получим
. Применяя граничные условия, получим  .
.
б) Если 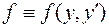 , т.е.
, т.е. 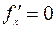 и
и 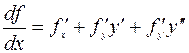 . Из уравнения Э-Л (7.2.2) следует, что
. Из уравнения Э-Л (7.2.2) следует, что
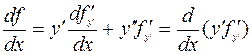 ,
,
и, таким образом, 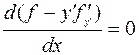 . Следовательно,
. Следовательно, 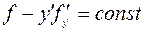 есть первый интеграл.
есть первый интеграл.
в) Если 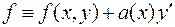 , то уравнение Э-Л упрощается и имеет вид
, то уравнение Э-Л упрощается и имеет вид 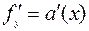 .
.
г) Если  , то
, то  , и тем самым
, и тем самым  , т.е. экстремали являются прямыми вида
, т.е. экстремали являются прямыми вида  .
.
Так как уравнение Эйлера–Лагранжа представляет собой только необходимое условие экстремума, то экстремали не всегда реализуют минимум или максимум функционала. Приводимые далее необходимые условия экстремума позволяют в определенных случаях исключить те экстремали, которые не дают экстремума функционалу.
Условие Лежандра. Используя вторую вариацию 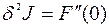 , получаем необходимое условие экстремума Лежандра: чтобы функция
, получаем необходимое условие экстремума Лежандра: чтобы функция  доставляла слабый (локальный) минимум (максимум) функционалу
доставляла слабый (локальный) минимум (максимум) функционалу 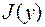 , необходимо, чтобы для
, необходимо, чтобы для 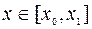 имело место неравенство
имело место неравенство
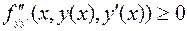
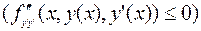
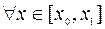 . (7.2.5)
. (7.2.5)
Пример 5. Найти минимум функционала
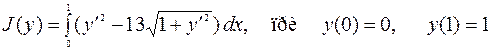 .
.
Так как подынтегральная функция зависит только от  , то экстремалями являются прямые. С учетом граничных условий получаем
, то экстремалями являются прямые. С учетом граничных условий получаем  . Условие Лежандра имеет вид
. Условие Лежандра имеет вид 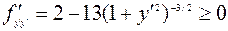 . Для экстремали
. Для экстремали  это неравенство не выполняется, поэтому слабого локального минимума не существует.
это неравенство не выполняется, поэтому слабого локального минимума не существует.
Условие Якоби. Пусть для функции  ,
, 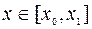 , выполнено строгое условие Лежандра, то есть
, выполнено строгое условие Лежандра, то есть 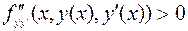 . Если при этом функционал
. Если при этом функционал 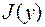 имеет при
имеет при  слабый минимум, то для точки
слабый минимум, то для точки  , сопряженной с
, сопряженной с 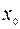 , должно выполнятся неравенство
, должно выполнятся неравенство 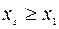 . Сопряженная точка
. Сопряженная точка  определяется следующим образом. Пусть
определяется следующим образом. Пусть 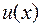 есть решение дифференциального уравнения Якоби
есть решение дифференциального уравнения Якоби
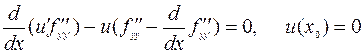 . (7.2.6)
. (7.2.6)
За  принимаем наименьший из корней функции
принимаем наименьший из корней функции 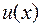 , лежащих справа от x0. Если справа от
, лежащих справа от x0. Если справа от 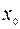 нет корней то полагаем
нет корней то полагаем  .
.
Пример 6. Найти минимум функционала
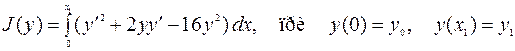 .
.
Уравнение Эйлера –Лагранжа 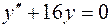 имеет решение
имеет решение 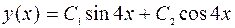 . Условие Лежандра выполнено в строгой форме
. Условие Лежандра выполнено в строгой форме
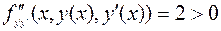 .
.
Уравнение Якоби (7.2.6) имеет вид
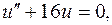
 .
.
Его решение 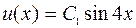 . Поэтому для сопряженной точки получаем значение
. Поэтому для сопряженной точки получаем значение 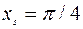 , то есть условие Якоби выполнено в случае, если
, то есть условие Якоби выполнено в случае, если 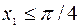 .
.






