Сформулируем задачу оптимального управления. Пусть требуется минимизировать функционал
(8.1.1)
при условиях
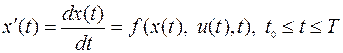, (8.1.2)
, (8.1.3)
, 
, 
(8.1.4)
, 
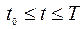. (8.1.5)
Здесь:
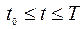- – отрезок времени между концами промежутка;
- 
– вектор фазовых переменных определяет состояние системы в момент времени t;
- 
– вектор переменных управления в момент времени t для воздействия на состояния системы;
- 
– заданная вектор-функция;
- 
, 
– заданные функции,
- ограничения (8.1.2) задают уравнения движения,
- (8.1.3) – ограничения на фазовые переменные в каждый момент времени, где 
– множество, определенное для каждого момента времени,
- (8.1.4) – ограничения на фазовые переменные и время на концах промежутка времени, где 
, 
– заданные функции, 
, 
– заданные множества;
- (8.1.5) – ограничения на переменные управления, где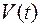 
–множество, определенное для каждого момента времени промежутка.
В учебной литературе символом 
обозначают как функцию в целом, так и ее конкретное значение в точке t. Там, где это необходимо функцию 
мы будем обозначать 
или просто z.
Функция называется кусочно-непрерывной на отрезке 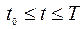, если она непрерывна во всех точках отрезка, за исключением быт может конечного числа точек.
Мы будем предполагать, что функция 
определена и кусочно-непрерывна на отрезке 
. Выбором параметров управления можно влиять на движение объекта.
Фазовые координаты x, определяемые согласно (8.1.2) будут определены в виде функции времени на отрезке 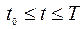, если заданы функция управления и левый конец траектории
. (8.1.6)
Решение задачи Коши (8.1.2), (8.1.6) (траекторию движения управляемой системы) будем обозначать
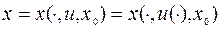или 
.
Пара векторных функций, (x (×), u (×)), где u (×) – управление, а x (×) – соответствующая этому управлению фазовая траектория называется процессом управления.
В случаях, когда ясно, какому управлению или начальному условию (8.1.6) соответствует траектория, то в ее обозначении эти параметры будут опускаться. Начальную точку 
назовем левым концом траектории, 
– начальным моментом, 
– правым концом траектории, T – конечным моментом.
Типы задач оптимального управления можно разбить на 3 группы, которые определяются способом задания характеристик.
1. Функционала (8.1.1).
2. Ограничений вдоль траекториии (8.1.3), (8.1.5).
3. Краевых условий (8.1.4).
Способы задания функционала.
а) Задача Лагранжа:
(8.1.7)
б) Задача Майера:
(8.1.8)
в) Задача Больца:
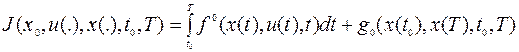(8.1.1)
г) Задачи на быстродействие, это задачи, где минимизируемым функционалом является время 
.
д) Если 
, 
, множества , , , 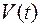не зависят от времени, то задачу (8.1.1)-(8.1.5) называют автономной или стационарной.
Для автономной управляемой системы при сдвиге вдоль оси времени свойства управлений не меняются.
Способы задания краевых условий (8.1.4), т.е. условий которым удовлетворяют концы траекторий.
1) Начальный момент закреплен, если множество состоит из одной точки 
.
2) Конечный момент закреплен, если множество состоит из одной точки Т.
3) Если 
[или 
] то говорят, что левый [правый ] конец закреплен.
4) Если 
[или 
] то говорят, что левый [правый ] конец свободен.
5) В остальных случаях называют левый [правый ] конец подвижным.
Набор 
называется допустимым, если функция 
определена и кусочно-непрерывна на отрезке и для него выполняются ограничения (8.1.2)-(8.1.5).
Допустимый набор 
назовем решением задачи оптимального управления, если функционал (8.1.1) на этом наборе достигает минимума.
Если движение управляемого объекта при заданных начальных условиях вполне точно и однозначно определяется выбором управляющих параметров в каждый момент времени, система называется детерминированной.
Если в процесс управления системой «вмешиваются» случайные факторы, воздействие которых может быть оценено лишь с некоторой вероятностью, система называется стохастической.
Совокупность всех точек пространства Rn, в каждую из которых может быть приведена управляемая система из начального состояния x 0 в момент времени T с помощью допустимого управления 
. называется множеством достижимости.
Приведем формулировки некоторых линейных задач оптимального управления.
Линейная задача оптимального управления автономной системой имеет следующий вид:
x (0) = x 0;
u (t)Î U Ì Rm, 0 £ t £ T;
x (T)Î M (T);
;
Линейная неавтономная задача оптимального быстродействия имеет следующий вид:
x (0) = x 0;
u (t)Î U Ì Rm, 0 £ t £ T;
x (T)Î M (T);
T ® min.
