Общая задача нелинейного программирования имеет вид:
 ,
,
 (6.6.1)
(6.6.1)

где все функции предполагаются дифференцируемыми.
1. Необходимые условия минимума. Для произвольной допустимой точки  введем множества индексов
введем множества индексов
 , (активные ограничения неравенства)
, (активные ограничения неравенства)
 , (все активные ограничения). (6.6.2)
, (все активные ограничения). (6.6.2)
Теорема 21 (Каруш-Джон). Пусть  – точка локального минимума в (6.6.1), а функции
– точка локального минимума в (6.6.1), а функции 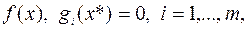 непрерывно дифференцируемы в окрестности
непрерывно дифференцируемы в окрестности  . Тогда найдутся числа
. Тогда найдутся числа  не все равные 0, такие, что
не все равные 0, такие, что  и
и
 . (6.6.3)
. (6.6.3)
Введем функцию Лагранжа

где  ,
,  .
.
Выражение (6.6.3) называется условием стационарности. Его можно записать в виде
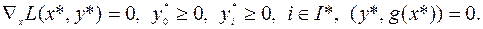 (6.6.3)
(6.6.3)
Согласно теореме 1 в точке локального минимума должны выполняться условия:
1) условия стационарности 
2) условия допустимости 
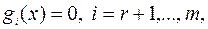
3) условия неотрицательности 
4) условие нетривиальности  ,
,
5) условие дополняющей нежесткости 
Перечисленные условия дают сумму соотношений, которые необходимо выполнить при поиске возможных точек минимума.
Сформулируем условия, при которых можно гарантировать  .
.
Условие регулярности. Векторы  , линейно независимы.
, линейно независимы.
Теорема 22. Пусть  – точка локального минимума в (6.6.1), функции
– точка локального минимума в (6.6.1), функции  непрерывно дифференцируемы в окрестности
непрерывно дифференцируемы в окрестности  , и выполнены условия регулярности. Тогда найдутся числа
, и выполнены условия регулярности. Тогда найдутся числа  , такие, что
, такие, что

 ,
, 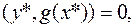 (6.6.4)
(6.6.4)
где 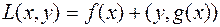
2. Достаточные условия минимума для некоторой точки позволяют утверждать, что она является точкой минимума.
Теорема 23. Пусть  – допустимая точка, функции
– допустимая точка, функции  дважды дифференцируемы в
дважды дифференцируемы в  . Пусть для некоторого
. Пусть для некоторого  выполняется (6.6.4) и для некоторого
выполняется (6.6.4) и для некоторого  , для которого
, для которого
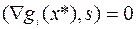 ,
,  ,
,
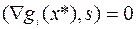 ,
,  , (6.6.5)
, (6.6.5)
 ,
,  ,
,
выполняется неравенство
 .
.
Тогда  – точка локального минимума в задаче (6.6.1).
– точка локального минимума в задаче (6.6.1).
Пример 1. Пусть требуется решить задачу минимизации
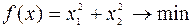 , (6.6.6)
, (6.6.6)
при ограничениях
 . (6.6.7)
. (6.6.7)
Решение. В силу присутствия одного ограничения будет выполнено условие регулярности в виде линейной независимости градиентов ограничений в произвольной точке. Поэтому для поиска подозрительных на минимум точек используем необходимые условия

 ,
, 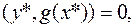 (6.6.8)
(6.6.8)
для функции Лагранжа, записанной в виде
 .
.
В результате получим

Решая систему уравнений, и исключая  , получим взаимосвязь переменных
, получим взаимосвязь переменных  .
.
На основе условия допустимости, т.е. выполнимости ограничения (6.6.7), с учетом взаимосвязи  , получим
, получим  , т.е.
, т.е.  .
.
Матрица вторых производных функции Лагранжа имеет вид
 .
.
В силу неравенства  для произвольного s и произвольной точки пространства переменных, согласно теореме о достаточных условиях оптимальности, точка
для произвольного s и произвольной точки пространства переменных, согласно теореме о достаточных условиях оптимальности, точка  является точкой минимума.
является точкой минимума.
Методы нелинейного программирования получаются из методов минимизации при ограничениях равенствах и неравенствах посредством соответствующих линейных комбинаций.
Глава 7. Основы вариационного исчисления (ВИ)
Постановка задачи, примеры и основные понятия
Вариационное исчисление - математическая дисциплина, посвященная отысканию экстремальных (наибольших или наименьших) значений функционалов. Под функционалом понимается числовая функция, определенная на некоторых классах функций. Функционал ставит в соответствие каждой функции из такого класса некоторое число. Примером функционала является интеграл  , где
, где 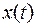 - непрерывная функция, определенная на отрезке
- непрерывная функция, определенная на отрезке  . Вариационное исчисление является развитием той части математического анализа, которая посвящена отысканию экстремумов функций.
. Вариационное исчисление является развитием той части математического анализа, которая посвящена отысканию экстремумов функций.
Пример 1 (задача о брахистохроне). Между точками  и
и  , расположенными на различной высоте, нужно провести соединяющую их кривую таким образом, чтобы время падения тела, движущегося без трения вдоль кривой из
, расположенными на различной высоте, нужно провести соединяющую их кривую таким образом, чтобы время падения тела, движущегося без трения вдоль кривой из  в
в  под действием силы тяжести было минимальным.
под действием силы тяжести было минимальным.

Рис. 1. Задача о брахистохроне
Поместим начало координат в точку  и направим оси координат как показано на рис. 1. Предположим, что тело находится в момент начала падения в состоянии покоя. Из закона сохранения энергии следует, что
и направим оси координат как показано на рис. 1. Предположим, что тело находится в момент начала падения в состоянии покоя. Из закона сохранения энергии следует, что
 ,
,
откуда для скорости  имеем
имеем  , и тем самым время падения
, и тем самым время падения  (с учетом, что
(с учетом, что  ) выражается интегралом
) выражается интегралом
 .
.
Требуется найти функцию  , график которой точки
, график которой точки  и
и  , то есть
, то есть  и
и  , и которая минимизирует указанный интеграл.
, и которая минимизирует указанный интеграл.
Пример 2. Найти кратчайшее расстояние между двумя точками 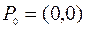 и
и  в плоскости
в плоскости  ,
,  , т.е. найти функцию
, т.е. найти функцию  , при которой
, при которой

принимает наименьшее значение. При этом  должна удовлетворять условиям
должна удовлетворять условиям  и
и  .
.
В приведенных примерах отыскиваются функции  , которые минимизируют функционал вида:
, которые минимизируют функционал вида:
 (7.1.1)
(7.1.1)
при граничных условиях:
 ,
,  . (7.1.2)
. (7.1.2)
Задача (7.1.1), (7.1.2) - так называемая простейшая задача вариационного исчисления.
Будем рассматривать функции  из класса непрерывных и непрерывно дифференцируемых функций на
из класса непрерывных и непрерывно дифференцируемых функций на  , которые будем обозначать
, которые будем обозначать  и
и  соответственно. Определим нормы в
соответственно. Определим нормы в  и
и  . Аналогом расстояния между двумя функциями в каждом из классов является норма разности этих функций. Понятие нормы определяется следующим образом:
. Аналогом расстояния между двумя функциями в каждом из классов является норма разности этих функций. Понятие нормы определяется следующим образом:
в  :
:  ; (7.1.3)
; (7.1.3)
в  :
:  . (7.1.4)
. (7.1.4)
В качестве  –окрестности
–окрестности  функции
функции  понимают тождество
понимают тождество
 (7.1.5)
(7.1.5)
Если для функции  из области определения
из области определения 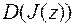 существует окрестность
существует окрестность  такая, что
такая, что
 или
или 
 , (7.1.6)
, (7.1.6)
то  называют (локальным) минимумом или максимумом. Элементы из
называют (локальным) минимумом или максимумом. Элементы из  называются также функциями сравнения.
называются также функциями сравнения.
Максимум (минимум) называется сильным, если в (7.1.6) принята норма на  . Максимум (минимум) называется слабым если в (7.1.6) сравнение кривых происходит в смысле нормы
. Максимум (минимум) называется слабым если в (7.1.6) сравнение кривых происходит в смысле нормы  .
.
Глобальным максимумом (минимумом) называют число  для функции
для функции  , если
, если
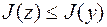

 . (7.1.7)
. (7.1.7)
Из определения экстремума и норм следует, что сильный экстремум одновременно является слабым.
Основным элементом исследования в ВИ являются понятия первой и второй вариации функционала.
Положим  и рассмотрим первую и вторую производные функции
и рассмотрим первую и вторую производные функции  по параметру
по параметру 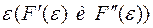 при
при  . Величины
. Величины  и
и 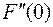 называются первой и второй вариацией функционала
называются первой и второй вариацией функционала 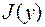 и обозначают соответственно
и обозначают соответственно 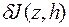 и
и  .
.
Условия 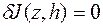 и
и 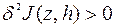
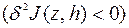 могут быть использованы при формулировке необходимых условий экстремума функционала
могут быть использованы при формулировке необходимых условий экстремума функционала 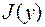 .
.






