Постановка задачи. Рассмотрим задачу оптимального управления со свободным правым концом и фиксированным временем. Пусть требуется минимизировать функцию
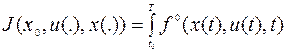 (8.2.1)
(8.2.1)
при условиях
 , (8.2.2)
, (8.2.2)
 ,
, 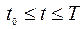 , (8.2.3)
, (8.2.3)
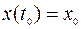 ,
,  заданы. (8.2.4)
заданы. (8.2.4)
где моменты  предполагаются заданными, управление является кусочно-непрерывной функцией, множества допустимых управлленний V не зависят от времени, фазовые ограничения заданы только на начальном конце отрезка.
предполагаются заданными, управление является кусочно-непрерывной функцией, множества допустимых управлленний V не зависят от времени, фазовые ограничения заданы только на начальном конце отрезка.
Для  обозначим частные производные
обозначим частные производные
 ,
,
 ,
, 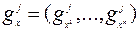 ,
, 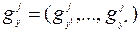
Сопряженная система. Введем сопряженную систему
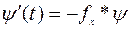 , (8.2.5)
, (8.2.5)
где 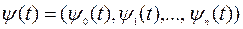 ,
,  ,
, 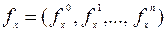 ,
, 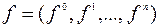 , или в координатной форме
, или в координатной форме
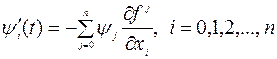 . (8.2.5)
. (8.2.5)
Подчиним выбор сопряженной вектор-функции условию
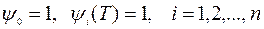 . (8.2.6)
. (8.2.6)
Введем функцию, называемую функцией Гамильтона
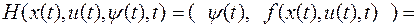
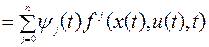 (8.2.7)
(8.2.7)
Вывод принципа максимума опирается на исследование условий при которых вариации функционала (8.2.1) в точке оптимума были бы неотрицательны

для любых допустимых вариаций 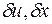 .
.






