Метод линеаризации. В этом методе на каждой итерации ограничения и минимизируемая функция линеаризуются и добавляется квадратичный член для получения ограниченной задачи. Очередное приближение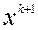 
есть решение линеаризованной задачи минимизации при линеаризованных ограничениях
(6.3.1)
Теорема 12. Пусть 
– точка невырожденного минимума в задаче (6.2.1), а 
удовлетворяют условию Липшица в окрестности . Тогда существует 
такое, что при 
метод (6.3.1) корректно определен и локально сходится к со скоростью геометрической прогрессии.
Задачу (6.2.1), используя правило множителей Лагранжа в форме (6.2.5)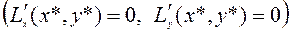 
сведем к решению системы уравнений
(6.3.2)
Решение системы (6.3.2) 
дает решение 
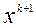задачи (6.2.1) и оценки двойственных переменных – множителей Лагранжа 
.
Двойственные методы. В этих методах используется факт, что в стационарной точке функции Лагранжа достигается минимум по переменным и максимум по переменным. В методе Эрроу-Гурвица
,
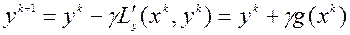(6.3.3)
делается шаг градиентного метода по переменным 
и 
.
Теорема 13. Пусть – точка невырожденного минимума в задаче (6.2.1), 
и вторые производные 
удовлетворяют условию Липшица в окрестности . Тогда найдется такое, что при метод (6.3.3) локально сходится к 
со скоростью геометрической прогрессии.
Модификация метода (6.3.3) состоит в полной минимизации по
(6.3.4)
Для метода (6.3.4) справедлива теорема 13, но при достаточно близком начальном приближении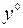 
к минимуму .
Методы модифицированной функции Лагранжа. Методы (6.3.3)- (6.3.4), основанные на модифицированной функции Лагранжа
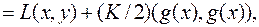(6.3.5)
обладают лучшими свойствами, поскольку условия экстремума (6.2.10) 
определяют точку минимума задачи (6.2.1) , как точку минимума функции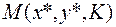 
в случаях, когда условия (6.2.5) 
определяют ее как стационарную точку. Аналог метода (6.3.3)
(6.3.6)
Теорема 14. Пусть – точка невырожденного минимума в задаче (6.2.1), вторые производные удовлетворяют условию Липшица в окрестности . Тогда при достаточно больших 
найдется такое, что при 
метод (6.3.6) локально сходится к 
со скоростью геометрической прогрессии.
Аналогом метода (6.3.4) является метод с полной минимизации по
(6.3.7)
Теорема 15. Пусть выполнены условия теоремы 3. Тогда для всякого 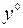, достаточно близкого к , найдется 
такое, что при 
метод (6.3.7) сходится к со скоростью геометрической прогрессии, знаменатель которой 
.
Метод штрафных функций имеет вид
. (6.3.8)
Теорема 16. Пусть задача (6.2.1) имеет решения, их множество обозначим 
. Пусть 
непрерывны, 
ограничено и замкнуто, 
. Тогда всякая предельная точка метода (6.3.8) (в задаче (6.3.8) предполагается вычисление глобального минимума) является глобальным минимумом для задачи (6.2.1).
Здесь – некоторое ограниченное замкнутое множество локализации минимума, введенное для того, чтобы решение задачи безусловной минимизации существовало.
Следует отметить надежность метода штрафных функций в зависимости от начального приближения. Поэтому его можно использовать на первом этапе, а более быстрый метод модифицированной функции Лагранжа – на втором.
