Приведем некоторые методы решения задачи выпуклого программирования (6.4.1).
Метод линеаризации. В этом методе на каждой итерации ограничения и минимизируемая функция линеаризуются и добавляется квадратичный член для получения ограниченной задачи. Очередное приближение 
есть решение линеаризованной задачи минимизации при линеаризованных ограничениях
(6.5.1)
Теорема 20. Пусть множество 
решений задачи (6.4.1) не пусто, функции 
выпуклы и дифференцируемы, а их градиенты удовлетворяют условию Липшица, и выполняется условие Слейтера. Тогда найдется 
такое, что при 
метод (6.5.1) сходится к 
. Если при этом функция 
сильно выпукла, то 
, 
.
В методе (6.5.1) учитываются все ограничения. Можно в (6.5.1) учитывать только наиболее нарушенные ограничения из множества
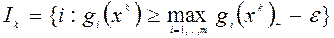(6.5.2)
