Наиболее простая задача условной минимизации имеет вид
, (6.1.1)
где 
– множество простой структуры. Например, параллелепипед 
, шар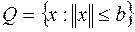 
, линейное многообразие 
.
Условия экстремума. Точка 
называется локальной точкой минимума (или просто точкой минимума) в задаче (6.1.1),
если 
при некотором 
.
Если 
то 
– точка глобального минимума.
Множество называется выпуклым,
если при 
точка 
для 
.
Теорема 1 (необходимое условие минимума 1 порядка). Пусть 
дифференцируема в точке минимумаx 
, а –выпуклое множество. Тогда
. (6.1.2)
Доказательство производится от противного. Предполагается, что существует точка не удовлетворяющая (6.1.2). На основе этого предположения на луче 
находится точка с меньшим значением функции, что противоречит предположению, что 
– точка минимума.
Условие (6.1.2) означает, что множество и множество 
, образованное направлениями локального убывания 
не должны пересекаться.
Для выпуклой удается сформулировать достаточное условие экстремума в терминах первой производной.
Теорема 2 (достаточное условие минимума 1 порядка). Пусть дифференцируема в точке 
, –выпуклое множество и выполняется условие
,
. (6.1.3)
Тогда –точка локального минимума на .
В условиях теоремы 2 минимум достигается на границе.
Теорема 3 (Необходимое и достаточное условие минимума 1 порядка). Пусть выпуклая на 
и дифференцируемая в точке 
функция. Тогда условие
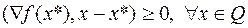, (6.1.4)
является необходимым и достаточным для того, чтобы был глобальным минимумом на .
Существование и единственность минимума.
Теорема 4 (Вейерштрасса). Пусть –непрерывная на 
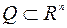, множество замкнуто, а множество 
ограничено и непусто для некоторого 
. Тогда задача (6.1.1) имеет решение.
Если выполняется достаточное условие минимума (6.1.3), то минимум единственный.
Теорема 5 . В условиях теоремы 2 –локально единственная точка минимума.
Как и в случае минимизации без ограничений, единственность решения гарантируется строгой выпуклостью функции .
Дадим изложение основных методов решения задачи (6.1.1).
Метод проекции градиентаявляется обобщением градиентного метода, в котором выход за множество ограничений всякий раз компенсируется посредством перехода в точку проекции
, (6.1.5)
где операция проектирования определена выражением
. (6.1.6)
Теорема 6. Пусть – выпуклая дифференцируемая функция в , градиент которой удовлетворяет условию Липшица с константой 
. Пусть выпуклое и замкнутое, 
и 
. Тогда:
а) 
;
б) если сильно выпукла, то 
со скоростью геометрической прогрессии;
в) если дважды дифференцируема и 
, то знаменатель прогрессии равен 
;
Метод условного градиента. В его основе лежит идея линеаризации функции и использование линеаризации для вычисления направления спуска посредством минимизации методом проекции градиента полученной линейной функции на множестве
, (6.1.7)
. (6.1.8)
Предполагается что задача минимизации (6.1.7) имеет решение, что решение может быть найдено достаточно просто и указано правило выбора шагового множителя 
.
Теорема 7. Пусть f(x) – выпуклая дифференцируемая функция в , градиент которой удовлетворяет условию Липшица с константой . Пусть выпуклое и замкнутое, 
и 
. Тогда предельные точки 
последовательности 
– точки минимума 
и справедливы оценки:
(6.1.9)
(6.1.10)
