В градиентном методе минимизации основой является идея локальной аппроксимации минимизируемой функции. Если функция дважды дифференцируема, то можно для поиска последовательных приближений использовать ее квадратичное приближение в точке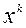 
.
.
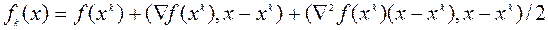При условии 
функция 
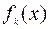имеет единственную точку минимума.
,
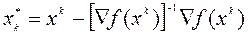которую можно принять в качестве последующего приближения, либо использовать для получения направления спуска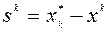 
. Суммируя сказанное, получим метод Ньютона
(5.8.1)
где величина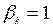 
, либо определяется из условия одномерной минимизации (5.4.8).
При условии минимизации сильно выпуклой функции, градиент которой удовлетворяет условию Липшица, для последовательности 
, генерируемой процессом (5.8.1) при условии (5.4.8), справедлива оценка (5.7.2). Если дополнительно матрица Гессе удовлетворяет условию Липшица, то последовательность , генерируемая процессом (2.8.3), сходится к 
квадратично.
Последнее свойство является следствием использования квадратичной модели для приближения минимизируемой функции. Подавляющее большинство эффективных методов минимизации гладких функций основано на использовании квадратичной модели для последующих приближений минимума, параметры которой оцениваются в процессе минимизации.
