Метод сопряженных градиентов (МСГ) первоначально предложен как метод минимизации квадратичной формы
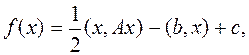(5.9.1)
где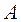 
– симметричная и строго положительно определенная 
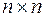матрица (в дальнейшем эти свойства матрицы будем обозначать 
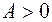). Для минимизации произвольных функций метод сопряженных градиентов записывается в виде
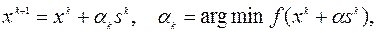
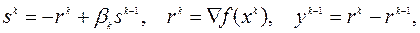(5.9.2)
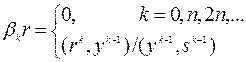
Векторы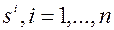 
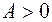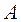называются сопряженными относительно матрицы или - ортогональными, если они удовлетворяют условиям
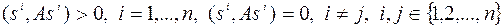(5.9.3)
Задача минимизации квадратичной формы (5.9.1) может быть решена за цикл точной одномерной минимизации вдоль сопряженных векторов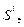 
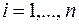, из произвольной начальной точки 
.
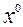Если метод (5.9.2) применяется для квадратичной функции (5.9.1), где 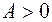, то векторы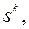 
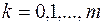, где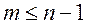 
, будут сопряженными.
Теорема 9. Метод (5.9.2) находит точку минимума квадратичной функции 
вида (5.9.1), где 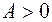, за число итераций не превосходящее 
.
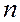При минимизации достаточно гладких функций МСГ сходится с квадратичной скоростью.
Теорема 10. Пусть 
-невырожденная точка минимума, и в ее окрестности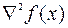 
удовлетворяет условию Липшица. Тогда для метода (5.9.2) в окрестности справедлива оценка:
.
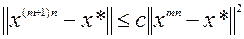Вследствие ошибок округления процесс (5.9.2), даже для квадратичной функции, не будет конечным. Особенно процесс (5.9.2) чувствителен к точности операции определения минимума вдоль направления. В связи со сказанным выше итерации (5.9.2) проводят до тех пор, пока не будет достигнута требуемая точность, а обновление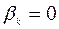 
проводится, особенно для большеразмерных задач, через m итераций, где 
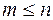. МСГ применяется в основном для решения большеразмерных задач в силу малой требуемой памяти для хранения параметров метода.
