Метод спуска, в котором направление 
, называется методом градиентного спуска. В этом методе для решения задачи (5.4.1) последовательные приближения строятся по формуле:
(5.7.1)
начиная из некоторой начальной точки (заданной) 
, а параметры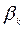 
определяются из условий одномерной минимизации (5.4.8). К методу (5.7.1) можно прийти, основываясь на приближении функции 
в точке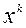 
линейной моделью (5.4.4), отыскивая решение вспомогательной задачи:
.
При минимизации сильно выпуклых функций, градиент которых удовлетворяет условию Липшица, согласно оценкам (5.5.1)-(5.5.2), сходимость к точке минимума 
последовательности 
, генерируемой процессом (5.7.1), определяется неравенством:
. (5.7.2)
Процедура минимизации (5.7.1) редко применяется на практике вследствие медленной сходимости. Она служит моделью для более эффективных методов.
