Теорема 8. Пусть:
1) функция 
сильно выпуклая, непрерывно дифференцируемая, ее градиент удовлетворяет условию Липшица;
2) последовательность 
строится по формулам (5.4.2) 
;
3) величины (3,4,6) удовлетворяют неравенствам 
.
4) параметры 
в (5.4.8) удовлетворяют условию 
.
Тогда справедливы оценки:
, (5.5.1)
, (5.5.2)
где 
.
Доказательство. На основании неравенства (3.1.13)
, (5.5.3)
справедливого для выпуклых функций, градиент которых удовлетворяет условию Липшица, получим нижнюю оценку возможного убывания функции
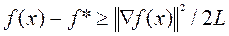, (5.5.4)
которое справедливо и для одномерной функции 
. Поэтому
, (5.5.5)
где 
- минимум по 
функции 
.
На основании неравенства (3.1.11)
(5.5.6)
найдем верхнюю оценку возможного убывания функции
. (5.5.7)
Из (5.5.5), в силу (5.4.8), будем иметь
Отсюда, на основании (5.5.7), получим
.
Следовательно
Используя рекуррентно полученное неравенство, придем к оценке (5.5.1). Оценка (5.5.2) следует из неравенства (3.1.8)
.
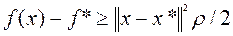