1. Задать начальное приближение 
.
Для 
выполнить действия:
2. В точке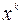 
выбрать направление спуска 
.
3. Произвести выбор шага спуска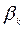 
.
4. Найти 
-ое приближение по формуле
. (5.4.2)
Релаксационные процессы. Процесс построения последовательности точек 
, назовем релаксационным, если
. (5.4.3)
В настоящем параграфе вопросы сходимости последовательности 
к минимуму функции исследуются в предположении релаксационности процесса спуска.
Выбор направления. В релаксационных методах спуска направление спуска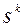 
выбирается таким образом, чтобы обеспечить возможность выполнения неравенства (5.4.3), по крайней мере, для малых значений 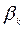. Для дифференцируемой функции в некоторой окрестности точки 
справедливо представление:
. (5.4.4)
Отсюда, при малых 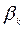в (5.4.2), убывание функции на итерации 
обеспечивается выбором направления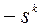 
из условия:
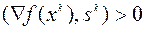. (5.4.5)
В большинстве эффективных методов спуска выбор направления связан с вычислением градиента минимизируемой функции в точке . На практике, при отсутствии процедур вычисления градиента, приходится пользоваться конечно-разностной аппроксимацией градиента по значениям функции.
Обозначим через 
величину косинуса угла между направлением антиградиента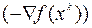 
, то есть направлением наискорейшего убывания функции 
в точке , и направлением спуска 
в точке .
. (5.4.6)
Условие 
, т.е. условие (3.2.5), является непременным условием выбора направления. При организации алгоритмов спуска на направление спуска накладывается более жесткое ограничение
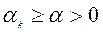, (5.4.7)
которое, в случае сильновыпуклых функций, гарантирует сходимость со скоростью геометрической прогрессии последовательности к минимуму. Если условие (5.4.7) не выполняется, то направление спуска соответствующим образом корректируется, с тем чтобы удовлетворить (5.4.7).
Выбор длины шага 
. С точки зрения оценок скорости сходимости методов спуска, как это мы увидим ниже, наилучшим является выбор из условия минимума функции вдоль направления . На практике применяют методы одномерной минимизации, гарантирующие лишь некоторую степень убывания функции
, (5.4.8)
где 
, при условии
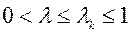, (5.4.9)
так как точное решение может оказаться неоправданно дорогим по затратам машинного времени.
В некоторых задачах минимизации условие точного одномерного спуска может ухудшить характеристики скорости сходимости процесса минимизации. Поэтому на практике проводится настройка параметров процедур одномерной минимизации на определенный класс практических задач.
