Подавляющее большинство методов минимизации относится к классу итеративных. Это означает, что с их помощью генерируются бесконечные последовательности 
, текущие приближения точки минимума 
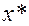. При этом работоспособность метода еще не гарантирована доказательством сходимости соответствующей последовательности. Нужна определенная скорость сходимости. Нельзя давать оценку алгоритму, основываясь лишь только на его теоретических оценках скорости сходимости, точно также, нельзя пренебрегать алгоритмом из-за отсутствия оценок скорости сходимости, поскольку возможно доказательства нет ввиду его сложности.
Рассмотрим последовательность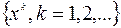 
сходящуюся к точке минимума 
. Будем предполагать, что все элементы последовательности различны и не совпадают с 
.
Последовательность называется сходящейся с порядком 
, если – максимальное число, для которого
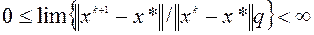. (5.3.1)
При 
говорят о линейной скорости сходимости или о сходимости со скоростью геометрической прогрессии, что может быть представлено в виде неравенства для достаточно больших 
, (5.3.2)
где 
, а при 
говорят о сверхлинейной скорости сходимости. При 
говорят о квадратичной скорости сходимости
. (5.3.3)
