Функция 
, называется выпуклой, если
. (5.1.1)
Функция , называется строго выпуклой, если в (5.1.1) при 
выполняется строгое неравенство. Функция 
, называется сильно выпуклой с константой 
, если при 
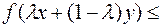
(5.1.2)
Для дифференцируемой функции выпуклость эквивалентна неравенству
(5.1.3)
строгая выпуклость – неравенству
, (5.1.4)
а сильная выпуклость – неравенству
(5.1.5)
Из неравенств (5.1.3)–(5.1.5) вытекают следствия:
а) для выпуклой функции выполняется неравенство
; (5.1.6)
б) для строго выпуклой функции при x ¹ y - строгое неравенство (5.1.6);
в) для сильно выпуклой функции
(5.1.7)
Для дважды дифференцируемой функции выпуклость эквивалентна условию 
, а сильная выпуклость – условию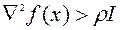 
для всех 
.
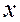Для дифференцируемой сильно выпуклой функции 
точка минимума 
(как мы увидим ниже) существует, единственна и 
. Поэтому из неравенств (5.1.5), (5.1.7) получим
, (5.1.8)
, (5.1.9)
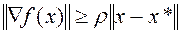. (5.1.10)
Для сильновыпуклой функции также справедлива оценка
. (5.1.11)
Согласно (5.1.11), возможное полное уменьшение функции в результате минимизации ограничено сверху.
Для дифференцируемой функции, градиент которой удовлетворяет условию Липшица
(5.1.12)
и 
, справедлива оценка
. (5.1.13)
Если функция выпукла и дифференцируема, а ее градиент удовлетворяет условию Липшица, тогда
(5.1.14)
