1. Задать начальное приближение  , и систему окрестностей
, и систему окрестностей 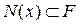 для
для  Положить
Положить  .
.
2. Найти точку минимума  функции
функции  в окрестности
в окрестности  .
.
3. Если, то { положить и перейти на п.2.}, иначе {останов}.
На практике бывает полезно осуществить локальный поиск из нескольких начальных точек. Поиск по окрестности в п.2. алгоритма может производится не полностью, а до первого улучшения уже имеющегося решения. В случае больших окрестностей и сложности задания правил перебора точек окрестности возможна организация случайного перебора точек окрестности.
Глава 5. Безусловная минимизация
В настоящее время известны сотни методов решения задачи безусловной минимизации:

 . (5.0.1)
. (5.0.1)
Ниже будут приведены основные принципы организации алгоритмов определенных типов и приведены некоторые из них.






