Рассмотрим задачу о кратчайшем пути в графе с неотрицательными весами дуг (рис.1). Ветвление в этой задаче - это выбор очередной дуги. В качестве нижней оценки примем суммарную длину частичного пути до некоторой вершины. На рис.2. приведены шаги ветвления в предположении, что ветвление производится для вершины из активного множества с наименьшей нижней оценкой. Шаги ветвления можно выразить схемой:
1. 
2. 
3. 
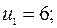
на шаге 3 получен первый “рекорд” 
Это позволяет исключить из активного множества вершину 
4. 
на этом шаге из активного множества исключаются вершины 
и 
5. Поскольку в активном множестве нет вершин, процесс закончен.
Рис.1. Задача о кратчайшем пути.
Рис.2. Дерево поиска, полученное при условии, что ветвление производится в вершине наименьшей нижней границы. 
- “рекорд”.
