Пример. Задача целочисленного линейного программирования (ЦЛП).
Задачей ЦЛП называют следующую задачу оптимизации:
- целочисленно.
Здесь 
, 
, 
. Элементы матрицы 
и векторов 
и 
предполагаются целыми. На рис.1 приведен пример двумерной задачи ЦЛП.
Рис.1. Четыре целочисленные точки, ближайшие к оптимуму задачи ЛП, недопустимы.
В некоторых приложениях дробные решения недопустимы, например, в приложении, где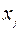 
- число самолетов, назначаемых на маршрут 
. Задачи ЛП, формулируемые как задачи ЦЛП, как правило, по своей природе не допускают подхода, основанного на округлении. Один из эффектов округления - это потеря допустимости решения (см. рис.1).
Пример. (Задача коммивояжера (ЗК)). Коммивояжеру необходимо объехать 
городов 
, начиная с города 1, и посещая каждый город ровно 1 раз, по самому короткому маршруту.
Обозначим 
матрицу расстояний между городами. Сопоставим дуге 
переменную 
и, положив 
, если дуга содержится в обходе, и в противном случае, можно сформулировать ЗК следующим образом:
(a) 
(4.1.1)
(б)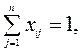 
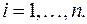
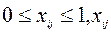- целые 
Равенства (а) выражают тот факт, что в каждую вершину входит ровно одна дуга, а равенства (б) - тот факт, что из каждой вершины выходит ровно одна дуга.
В действительности, задача (4.1.1) описывает задачу о назначении и содержит в своем допустимом множестве маршрутов маршруты, состоящие из нескольких замкнутых циклов. Нужны дополнительные ограничения для исключения подобных решений.
