Пусть имеется m пунктов производства с объемами производства 
, 
, и 
пунктов потребления с объемами потребления 
. Обозначим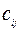 
- стоимость перевозки единицы продукции из пункта 
в пункт 
. Задача заключается в нахождении объемов перевозок 
из пунктов в пункты таких, что объемы перевозок из пунктов производства не превосходят объемов производства, в пунктах потребления полностью удовлетворяется спрос и общая стоимость перевозок минимальна.
(3.1.1)
(3.1.2)
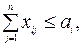
(3.1.3)
. (3.1.4)
Сбалансированная транспортная модель. Если общий объем производства совпадает с общим объемом потребления
(3.1.5)
тогда ограничения (3.1.2), (3.1.3) принимают вид
(3.1.6)
(3.1.7)
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения.
В случае превышения запасов над потребностью (потребностей над запасами) вводится фиктивный 
-й пункт назначения с потребностью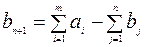 
(
-й пункт производства 
) и нулевыми тарифами перевозок.
