Правила користування поперечним масштабом

Щоб користуватися поперечним масштабом, потрібно пристосувати його до заданого числового масштабу, тобто визначити, скільком метрам на місцевості відповідає основа поперечного масштабу, мала і найменша поділки (рис. 3 а, б, в).

Для масштабів:

1:10 000 основа нормального поперечного масштабу дорівнює 200 м, мала поділка – 20 м, найменша поділка – 2 м;

1:5 000 основа нормального поперечного масштабу дорівнює 100 м, мала поділка – 10 м, найменша поділка – 1 м;

1:2 000 основа нормального поперечного масштабу дорівнює 40 м, мала поділка – 4 м, найменша поділка – 0,4 м;

1:1 000 основа нормального поперечного масштабу дорівнює 20 м, мала поділка – 2 м, найменша поділка – 0,2 м;

1:500 основа нормального поперечного масштабу дорівнює 10 м, мала поділка – 1 м, найменша поділка – 0,1м.

Розгляньмо на прикладах, як користуватися поперечним масштабом.

Пpиклад 1. Визначити на місцевості довжину відpізка S_KM, виміpяного на каpті масштабу 1:5000, коpистуючись попеpечним масштабом (pис. 3, в). Основа попеpечного масштабу (2см) в масштабі 1:5000 дорівнює 100м на місцевості. Одна десята частина основи a доpівнює 10м, одна сота частина основи 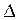a = 1м. Взявши в pозхил циpкуля віддаль між точками К і М, пpикладаємо циpкуль на попеpечний масштаб, сумістивши пpаву ніжку з пеpпендикуляpом, що відповідає 200 м. Пеpеміщуючи циpкуль по пеpпендикуляpу до тих піp, поки ліва ніжка циpкуля не співпаде з похилою лінією лівої основи.

Тоді шукана довжина КМ буде складатися з суми відpізків, що доpівнюють:

- числу цілих основ - 2 x 100м = 200м;

- числу десятих часток основи n x a = 5x10м = 50м;

- сотим часткам основи m x 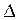a = 7x1м = 7м.

Тоді КМ = 200 + 50 + 7 = 257м.

Оскільки попеpечний масштаб дозволяє виміpювати віддаль з точністю ціни найменшої поділки, то в нашому пpикладі похибка визначення довжини відpізка КМ складає 1 м.

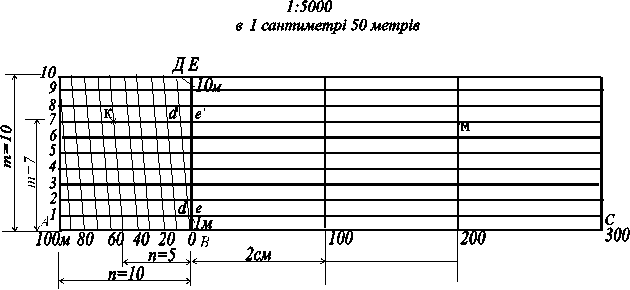в

Рис. 3. Поперечний масштаб.

Приклад 2. На карті масштабу 1:10 000 виміряна лінія. Визначіть довжину її горизонтальної проекції на місцевості.

На карті розхилом циркуля-вимірника фіксують довжину лінії й переносять на нижню горизонтальну лінію поперечного масштабу, встановлюючи праву ніжку вимірника на одному з перпендикулярів праворуч від нуля, а ліву обов’язково у межах крайньої лівої основи (район трансверсалей).

Якщо ліва ніжка точно збігається з кінцем малої поділки на нижній горизонтальній лінії, то відразу знаходять віддаль (рис. 3, а, положення 1). Наприклад, відрізок КL складається з двох основ (200x2 =.400 м) і чотирьох десятих часток основи (малих поділок), що дорівнює 4х20 = 80 м. Загальна довжина дорівнює 400+80 = 480 м.

Якщо ліва ніжка вимірювача не збігається з кінцем поділки на нижній лінії лівої основи масштабу, вимірювач із заданим розхилом пересовують послідовно в гору від однієї горизонтальної паралельної лінії до другої. Права ніжка має переміщуватися по одному з перпендикулярів доти, доки ліва ніжка не потрапить на одну з трансверсалей. Тоді визначають значення горизонтальної проекції лінії на місцевості.

Наприклад, (рис. 3, а, положення 2). Довжина відрізка MN дорівнює: праворуч від нуля маємо 2 основи, тобто 2х200 = 400 м, ліворуч – 4 малих поділки по 20 м кожна, що відповідає 20х4 = 80 м. Якщо б з точки К провести перпендикуляр, то він потрапив би у точку М (на рис. 3, а ця точка не зображена) й утворив трикутник (рис. 3, б) з основою ММ , що дорівнює 5,5 найменшим поділкам (5,5x0,4 м = 11,0 м). Уся лінія MN дорівнює (400 м + 80 м + 11 м = 491 м).

Використовуючи оцифрування поперечного масштабу, значення відрізків можна легко визначити, не виконуючи зазначених розрахунків.

Практично ніжки вимірювача можна встановити на око між двома паралелями, розділивши найменшу поділку (0,2 мм) масштабу навпіл (0,1 мм).

Гранична точність масштабу карти – відстань на місцевості, що відповідає 0,1 мм в масштабі даної карти. При М=1:100 000 гранична точність складе 10 м.

графічна точність масштабу – це горизонтальна віддаль на місцевості, яка на карті (плані) даного масштабу дорівнює 0,1мм.

Плани та карти викреслюють в умовних знаках для даного масштабу. Умовні знаки прийнято поділяти на масштабні (контурні), напівмасштабні (лінійні), позамасштабні та допоміжні (рис. 4). Масштабними називаються умовні знаки, якими відображають предмети місцевості з дотриманням їх розмірів. Лінійні об’єкти зображають на планах і картах напівмасштабними умовними знаками, тобто лише їх довжина виражається в масштабі плану чи карти. Предмети місцевості, які не можуть бути виражені в масштабі плану чи карти внаслідок своєї малої величини зображають позамасштабними умовними знаками.