“ема. ути ор≥Їнтуванн€. «ображенн€ рельЇфу
ћета: ¬ивчити початков≥ напр€мки, ознайомитис€ з особливост€ми зображенн€ рельЇфу на топограф≥чних картах, навчитис€ визначати напр€мки л≥н≥й, встановлювати звТ€зки м≥ж кутами ор≥Їнтуванн€, читати карту ≥ план, розвТ€зувати задач≥ за планами ≥ картами.
ѕерел≥к питань на практичне вивченн€:
| 1. ќсновн≥ параметри геодезичного ор≥Їнтуванн€ л≥н≥й |
| 2. –озвТ€зуванн€ пр€моњ та оберненоњ геодезичноњ задач≥ |
| 3. —пособи зображенн€ рельЇфу на планах ≥ картах |
| 4. ѕобудова вертикального проф≥лю л≥н≥њ за даних параметр≥в рельЇфу |
“еоретичн≥ та методичн≥ в≥домост≥:
ќр≥Їнтуванн€ л≥н≥й Ц це визначенн€ напр€мку л≥н≥њ в≥дносно ≥ншого напр€мку, прийн€того за початковий (вих≥дний). «а початковий напр€мок в геодез≥њ приймають ≥стинний, магн≥тний та осьовий мерид≥ани або л≥н≥њ паралельн≥ њм (дл€ осьового мерид≥ана це л≥н≥њ к≥лометровоњ с≥тки.
≤стинним азимутом  (рис. 1) називаЇтьс€ кут, €кий в≥драховуЇтьс€ в≥д п≥вн≥чного напр€му ≥стинного мерид≥ана або л≥н≥њ, що паралельна до нього, за годинниковою стр≥лкою до заданоњ л≥н≥њ (в межах в≥д 0 до 360
(рис. 1) називаЇтьс€ кут, €кий в≥драховуЇтьс€ в≥д п≥вн≥чного напр€му ≥стинного мерид≥ана або л≥н≥њ, що паралельна до нього, за годинниковою стр≥лкою до заданоњ л≥н≥њ (в межах в≥д 0 до 360  ).
).

–ис. 1. ≤стинний азимут.
ћагн≥тним азимутом  (рис. 2) називаЇтьс€ кут, €кий в≥драховуЇтьс€ в≥д п≥вн≥чного напр€му магн≥тного мерид≥ана або л≥н≥њ, що паралельна до нього, за годинниковою стр≥лкою до заданоњ л≥н≥њ (в межах в≥д 0 до 360
(рис. 2) називаЇтьс€ кут, €кий в≥драховуЇтьс€ в≥д п≥вн≥чного напр€му магн≥тного мерид≥ана або л≥н≥њ, що паралельна до нього, за годинниковою стр≥лкою до заданоњ л≥н≥њ (в межах в≥д 0 до 360  ).
).

–ис. 2. ћагн≥тний азимут.
ƒирекц≥йним кутом a  (рис. 3)називаЇтьс€ кут, €кий в≥драховують в≥д п≥вн≥чного напр€му осьового мерид≥ана або л≥н≥њ, що паралельна до нього, за годинниковою стр≥лкою до заданоњ л≥н≥њ (в межах в≥д 0 до 360
(рис. 3)називаЇтьс€ кут, €кий в≥драховують в≥д п≥вн≥чного напр€му осьового мерид≥ана або л≥н≥њ, що паралельна до нього, за годинниковою стр≥лкою до заданоњ л≥н≥њ (в межах в≥д 0 до 360  ).
).
ƒирекц≥йн≥ кути можуть бути пр€мими (a 1-2) ≥ оберненими (a 2-1).
Ќа в≥дм≥ну в≥д азимута дирекц≥йний кут л≥н≥њ в р≥зних точках залишаЇтьс€ пост≥йним, тому пр€мий ≥ обернений дирекц≥йн≥ кути в≥др≥зн€ютьс€ один в≥д одного на 180 ∞.
a 1-2= a 2-1±180∞
¬≥н зм≥нюЇтьс€ в≥д 0∞ до 360∞.

–ис. 3. ƒирекц≥йний кут.
Ќа аркушах карти л≥н≥њ, що паралельн≥ до осьового мерид≥ана, - це вертикальн≥ к≥лометров≥ л≥н≥њ. “ому, дл€ вим≥рюванн€ дирекц≥йного кута л≥н≥њ јЅ через початкову точку ј провод€ть пр€му, що паралельна найближч≥й вертикальн≥й к≥лометров≥й л≥н≥њ ≥ в≥д њњ п≥вн≥чного напр€му транспортиром вим≥рюють дирекц≥йний кут л≥н≥њ јЅ. јналог≥чно вим≥рюють дирекц≥йний кут л≥н≥њ Ѕ¬.
–умб r Ц це гострий кут, що в≥драховуЇтьс€ в≥д найближчого напр€мку осьового мерид≥ану до л≥н≥њ. ѕри камеральн≥й обробц≥ польових результат≥в, користуванн≥ тригонометричними таблиц€ми зручн≥ше використовувати румб, а не дирекц≥йний кут. –умб зм≥нюЇтьс€ в межах в≥д 0∞ до 90∞ ≥ супроводжуЇтьс€ назвою чверт≥. (рис. 4). Ќаприклад: rј¬ = 45∞30' ѕн—

–ис. 4. –умб.
«в'€зок м≥ж ор≥Їнтовними кутами. 1. «в'€зок м≥ж справжн≥м ј та магн≥тним јћ азимутами.

–ис. 5. «вТ€зок м≥ж ј та јћ.
зближенн€ мерид≥ан≥в  - кут м≥ж ≥стинним мерид≥аном ≥ л≥н≥Їю с≥тки.
- кут м≥ж ≥стинним мерид≥аном ≥ л≥н≥Їю с≥тки.
якщо точка знаходитьс€ на сх≥д в≥д осьового мерид≥ана, то значенн€  матиме в≥дТЇмний знак, €кщо на зах≥д Ц додатн≥й.
матиме в≥дТЇмний знак, €кщо на зах≥д Ц додатн≥й.
|
|
|
‘ормули зв'€зку м≥ж справжн≥м та магн≥тними азимутами мають такий вигл€д:
A=Aћ + dсх
A=Aћ Ц dз
ут м≥ж географ≥чним та магн≥тним мерид≥анами називаЇтьс€ магн≥тним схиленн€м d. (рис. 5). ћагн≥тне схиленн€ вважаЇтьс€ сх≥дним при в≥дхиленн≥ магн≥тноњ стр≥лки до сходу в≥д географ≥чного мерид≥ану ≥ зах≥дним при в≥дхиленн≥ до заходу.
2. «в'€зок м≥ж справжн≥м азимутом ј та дирекц≥йним кутом а. ‘ормули зв'€зку мають вигл€д:
a=ј + gсх
a=ј Ц gз
ƒл€ напр€м≥в, проведених з точок, що лежать на осьовому мерид≥ан≥, азимути та дирекц≥йн≥ кути зб≥гатимутьс€. ƒл€ решти напр€м≥в в≥др≥зн€ютьс€ на величину g Ц зближенн€ мерид≥ан≥в. «ближенн€ мерид≥ан≥в дл€ точок, розташованих до сходу в≥д осьового мерид≥ану Ц додатн≥, до заходуЦв≥д'Їмне (рис. 7).
«в'€зок дирекц≥йних кут≥в з магн≥тними азимутами маЇ такий вигл€д:
a=ј + b Ц g

–ис. 7. «вТ€зок м≥ж ј та a.
схиленн€ магн≥тноњ стр≥лки  Ц кут м≥ж магн≥тним та ≥стинним мерид≥анами.
Ц кут м≥ж магн≥тним та ≥стинним мерид≥анами.
схиленн€ магн≥тноњ стр≥лки  вважають додатн≥м, коли магн≥тний мерид≥ан в≥дхил€Їтьс€ на сх≥д в≥д ≥стинного мерид≥ана, в≥дТЇмним - коли магн≥тний мерид≥ан в≥дхил€Їтьс€ на зах≥д в≥д ≥стинного мерид≥ана.
вважають додатн≥м, коли магн≥тний мерид≥ан в≥дхил€Їтьс€ на сх≥д в≥д ≥стинного мерид≥ана, в≥дТЇмним - коли магн≥тний мерид≥ан в≥дхил€Їтьс€ на зах≥д в≥д ≥стинного мерид≥ана.
«в'€зок м≥ж дирекц≥йними кутами a ≥ румбами r. ‘ормули зв'€зку приведено на рис. 8.
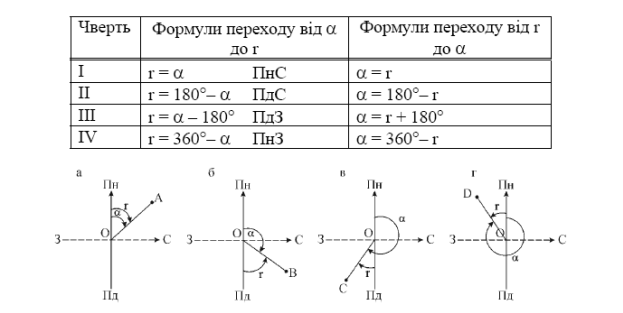
–ис. 8. «вТ€зок м≥ж a та r.
ћагн≥тний азимут на м≥сцевост≥ може бути вим≥р€ний за допомогою бусол≥.
ƒл€ визначенн€ ≥стинного та магн≥тного азимут≥в необх≥дно використати граф≥к, €кий розм≥щений п≥д п≥вденною рамкою карти з л≥воњ сторони в≥д числового масштабу (див. фрагмент карти). ѕо€сненн€ до граф≥ку подано на схем≥ (рис. 9)
¬раховуючи знаки  ≥
≥  , ≥стинний та магн≥тний азимути обчислюють за формулами
, ≥стинний та магн≥тний азимути обчислюють за формулами

 .
.
 .
.
|
ѕр€ма та обернена геодезична задач≥. ѕр€ма геодезична задача пол€гаЇ у визначенн≥ координат X2, Y2 точки 2 за в≥домими координатами X1, Y1 точки 1, в≥дстанню d м≥ж точками 1, 2 та дирекц≥йним кутом л≥н≥њ 1-2. (рис. 10). « трикутника 1a2 визначають прир≥ст координат:
DX1-2=d1-2Cos r1-2
DY1-2=d1-2Sin r1-2
«наки в приростах координат обирають зг≥дно з≥ знаками Sin та Cos. ƒал≥ визначаютьс€ координати точки 2 за формулами:
X2=X1+DX 1-2
Y2=Y1+DY1-2

–ис. 10. ѕр€ма геодезична задача.
ќбернена геодезична задача пол€гаЇ у визначенн≥ в≥дстан≥ d та дирекц≥йного кута a1-2 за в≥домими координатами двох точок ’1,Y1,’2,Y2.
« того ж трикутника (рис. 10) визначають румб напр€му 1 Ц 2 за формулами:
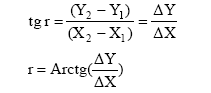
ƒирекц≥йний кут визначаЇтьс€ залежно в≥д чверт≥, €ка зумовлена знаками приросту координат D’, DY. √оризонтальне прокладанн€ л≥н≥њ 1Ц2 (в≥дстань d) визначаЇтьс€ за формулами:
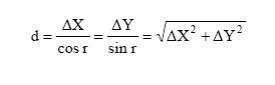
ќсобливост≥ вим≥рюванн€ кут≥в ≥ азимут≥в на топограф≥чн≥й карт≥ представлен≥ на рис. 11.


¬им≥рюванн€ дирец≥йного √еодезичний
кута за допомогою транспортиру транспортир


¬им≥рюванн€ на азимут≥в топограф≥чн≥й
карт≥ ¬изначенн€ по карт≥ дирекц≥йного,
розм≥щенн€ ор≥Їнтирних напр€м≥в
≥стинного ≥ магн≥тного азимут≥в
|

–ис. 11. ћетодолог≥€ визначенн€ кут≥в ≥ азимут≥в на топограф≥чн≥й карт≥.
ѕрактичн≥ завданн€:
«авданн€ 1. «а топограф≥чною картою N-34-37-¬-в («агор€ни) масштабу 1:25 000, користуючись транспортиром, вим≥р€ти дирекц≥йний кут (a) л≥н≥њ поданоњ в одному з вар≥ант≥в в таблиц≥ 1.
|
|
|
«авданн€ 2. ќбчислити ≥стинний азимут за вим≥р€ним в першому завданн≥ дирекц≥йним кутом ≥ зближенн€м мерид≥ан≥в, вказаним на карт≥ N-34-37-¬-в («агор€ни) масштабу 1:25 000.
ћетодичн≥ вказ≥вки. ќбчисленн€ ≥стинного азимута за дирекц≥йним кутом ≥ зближенн€м мерид≥ан≥в виконуЇтьс€ за формулою 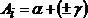 . «ближенн€м мерид≥ан≥в (g) називаЇтьс€ кут м≥ж ≥стинним мерид≥аном даноњ точки ≥ осьовим мерид≥аном зони, в €к≥й знаходитьс€ ц€ точка. ¬ сх≥дн≥й частин≥ зони зближенн€ мерид≥ан≥в буде додатн≥м, а в зах≥дн≥й Ц в≥дТЇмним. ќтже, при обчисленн≥ азимута в першому випадку потр≥бно зближенн€ мерид≥ан≥в g додати до дирекц≥йного кута a, а в другому Ц в≥дн€ти в≥д нього.
. «ближенн€м мерид≥ан≥в (g) називаЇтьс€ кут м≥ж ≥стинним мерид≥аном даноњ точки ≥ осьовим мерид≥аном зони, в €к≥й знаходитьс€ ц€ точка. ¬ сх≥дн≥й частин≥ зони зближенн€ мерид≥ан≥в буде додатн≥м, а в зах≥дн≥й Ц в≥дТЇмним. ќтже, при обчисленн≥ азимута в першому випадку потр≥бно зближенн€ мерид≥ан≥в g додати до дирекц≥йного кута a, а в другому Ц в≥дн€ти в≥д нього.
«авданн€ 3. ќбчислити дирекц≥йний кут за ≥стинним азимутом ≥ зближенн€м мерид≥ан≥в, €к≥ вказан≥ в одному з вар≥ант≥в в табл. 1.
«авданн€ 4. ќбчислити зворотний азимут за пр€мим азимутом ≥ зближенн€м мерид≥ан≥в, €к≥ вказан≥ в одному з вар≥ант≥в в табл. 1.
ћетодичн≥ вказ≥вки. јзимут, вим≥р€ний в початков≥й точц≥ л≥н≥њ, називаЇтьс€ пр€мим, а азимут, вим≥р€ний в к≥нцев≥й точц≥ Ц зворотним азимутом. якщо л≥н≥€ маЇ невелику довжину або проходить близько до напр€мку мерид≥ану, то зворотний азимут в≥др≥зн€Їтьс€ в≥д пр€мого на 180˚ ≥ може обчислюватись за формулою  . ¬ протилежному випадку, €кий маЇ м≥сце в умов≥ задач≥, необх≥дно враховувати зближенн€ мерид≥ан≥в ≥ обчислювати зворотний азимут за формулою
. ¬ протилежному випадку, €кий маЇ м≥сце в умов≥ задач≥, необх≥дно враховувати зближенн€ мерид≥ан≥в ≥ обчислювати зворотний азимут за формулою  . ѕри цьому зближенн€ мерид≥ан≥в g тут Ї кутом м≥ж мерид≥аном початковоњ ≥ к≥нцевоњ точок.
. ѕри цьому зближенн€ мерид≥ан≥в g тут Ї кутом м≥ж мерид≥аном початковоњ ≥ к≥нцевоњ точок.
3. —учасна карта повинна давати тривим≥рне у€вленн€ про м≥сцев≥сть, тобто, кр≥м вим≥р≥в у горизонтальн≥й площин≥, повинна давати можлив≥сть визначати види нер≥вностей земноњ поверхн≥, њх взаЇморозташуванн€ ≥ взаЇмозв'€зки; взаЇмоперевищенн€ ≥ абсолютн≥ висоти точок м≥сцевост≥, а також стр≥мк≥сть, форму ≥ довжину схил≥в.
–ельЇф - сукупн≥сть нер≥вностей земноњ поверхн≥, що складаютьс€ з р≥зноман≥тних елементарних форм р≥зного пор€дку.
–ельЇф Ї найб≥льш наочним на рельЇфних картах, але так≥ карти втрачають на точност≥ вим≥р≥в ≥ незручн≥ в користуванн≥.
—утн≥сть зображенн€ рельЇфу горизонтал€ми розгл€немо на такому приклад≥. ”€вимо остр≥в у вигл€д≥ гори. ” цьому положенн≥ берегова л≥н≥€ виходить у вигл€д≥ кривоњ ј¬. ѕроекц≥€ береговоњ л≥н≥њ на горизонтальну площину даЇ таку ж замкнену криву аb (рис. 12, 13).
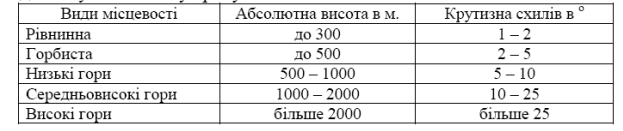
–ис. 12. “ип м≥сцевост≥ за характером рельЇфу.
“аблиц€ 1
¬их≥дн≥ дан≥ дл€ розрахунку практичних завдань
|
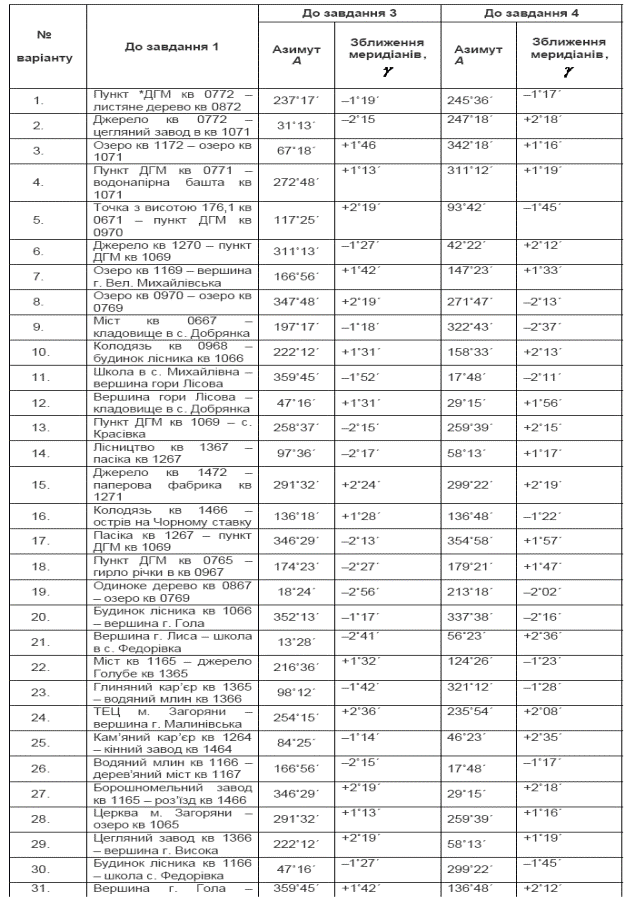
ѕродовженн€ табл. 1


–ис. 13. ѕоперечний перер≥з рельЇфу та характер його перевищень.
—пособи зображенн€ рельЇфу:
Ј —в≥тло-т≥ньове зображенн€ рельЇфу (випукл≥ форми рельЇфу б≥льш осв≥тлен≥, впадини Ц затемнен≥) (рис. 14);
Ј «а допомогою штрих≥в (рельЇф зображають виход€чи з принципу пр€мовисного осв≥тленн€ земноњ поверхн≥, при €кому вона буде менш осв≥тленою, коли крутизна схилу буде б≥льша. ¬≥дпов≥дно до крутизни схилу будуютьс€ шкали, де вказано сп≥вв≥дношенн€ товщини штриха до в≥дстан≥ м≥ж штрихами. ¬икористовувавс€ цей метод в 18-19 ст.);
Ј √≥псометричний (кожному д≥апазону висот в≥дпов≥даЇ певний кол≥р або його в≥дт≥нок);
Ј «а допомогою горизонталей (основний).


–ис. 14. —в≥тло-т≥ньове зображенн€ рельЇфу.
√оризонтал≥ Ц це л≥н≥њ, €к≥ зТЇднують точки з однаковими висотами. ¬они мають наступн≥ властивост≥.
Ј √оризонтал≥ Ц з≥мкнут≥ крив≥ в межах плану або карти;
Ј √оризонтал≥ на карт≥ або план≥ Ї неперервними л≥н≥€ми. ¬они можуть перериватись лише через €ри ≥ р≥ки.
Ј √оризонтал≥ не можуть перес≥катись ≥ розгалужуватись. ¬ин€тком може бути х≥ба нависла в горах скала;
Ј ¬≥ддаль м≥ж горизонтал€ми характеризуЇ крутизну схилу, тобто чим ближче розташован≥ горизонтал≥ на карт≥, тим крут≥ший схил. Ќапр€мок схилу позначаЇтьс€ схилштрихами (бергштрихами);
Ј √оризонтал≥ мають висоти, кратн≥ висот≥ перер≥зу рельЇфу. Ќаприклад, при перер≥з≥ рельЇфу 2,5м, горизонтал≥ будуть мати висоти 150м, 152,5м, 155м.
√оризонтал≥ зображуютьс€ на картах коричневим кольором ≥ бувають к≥лькох вид≥в (рис. 15).
|
|
|
1. ќсновн≥ (суц≥льн≥) горизонтал≥ - провод€тьс€ через висоту перер≥зу, служать дл€ в≥дображенн€ основних форм рельЇфу ≥ зображуютьс€ на карт≥ суц≥льною тонкою л≥н≥Їю.
2. ѕотовщен≥ горизонтал≥ служать дл€ полегшенн€ рахунку висот ≥ зручност≥ в читанн≥ рельЇфу; кожна п'€та основна горизонталь потовщуЇтьс€.
3. ƒодатков≥ (нап≥вгоризонтал≥) та
4. ƒопом≥жн≥ (чверт≥) горизонтал≥ служать дл€ в≥дображенн€ важливих подробиць рельЇфу, що не виражаютьс€ основними горизонтал€ми, ≥ провод€тьс€ через 1/2 та 1/4 висоти перер≥зу. «ображуютьс€ на картах переривчастими та короткими переривчастими л≥н≥€ми.

–ис. 15. ¬иди горизонталей: 1 - основн≥; 2 - потовщен≥; 3 - додатков≥; 4 - допом≥жн≥.
¬ивченн€ рельЇфу топограф≥чноњ карти починаЇтьс€ з визначенн€ напр€мк≥в п≥двищенн€ та зниженн€ м≥сцевост≥. ѕри цьому керуютьс€ наступними ознаками:
Ј схилштрихи (бергштрихи) завжди направлен≥ у сторону зниженн€ рельЇфу;
Ј основи цифр, €кими п≥дписан≥ горизонтал≥, зб≥гаютьс€ з напр€мком зниженн€ схилу;
Ј у напр€му водойм та водосток≥в м≥сцев≥сть знижуЇтьс€;
Ј стр≥мк≥сть схилу характеризуЇтьс€ величиною закладенн€ Ц в≥ддаллю м≥ж горизонтал€ми, чим б≥льша в≥ддаль Ц тим полог≥ший схил, ≥ навпаки, чим менша в≥ддаль Ц тим схил крут≥ший;
Ј горизонтал≥ згинаютьс€ на водорозд≥льних л≥н≥€х хребт≥в ≥ на тальвегах лощин.

–ис. 16. ’арактер направленост≥ ≥зол≥н≥й рельЇфу.
≈лементи рельЇфу, €к≥ не можна зобразити горизонтал€ми, викреслюють на картах спец≥альними умовними знаками (рис. 17, 18).

–ис. 17. «ображенн€ характерних форм рельЇфу на карт≥.

–ис. 18. 1 - насипи; 2 - вињмки на дорогах; 3 - курган; 4 - €ма; 5 -обрив; 6 - вимоњна; 7 -€р; 8- скел€-останець; 9 - вх≥д у печеру (грот); 10 - скел€.
ѕ≥д час pоботи з фpагментом каpти або плану висоту пеpетину pельЇфу можна визначити за числом ≥нтеpвал≥в n та пеpевищенн€м 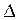 H м≥ж п≥дписаними гоpизонтал€ми. висоту пеpетину pельЇфу h обчислюють за фоpмулою
H м≥ж п≥дписаними гоpизонтал€ми. висоту пеpетину pельЇфу h обчислюють за фоpмулою
h = 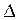 H / n
H / n
Ќапpиклад, число таких ≥нтеpвал≥в n = 4, а пеpевищенн€ м≥ж п≥дписаними горизонтал€ми 180м та 170м доp≥внюЇ  H =10 м (pис. 19). “од≥ дл€ даного прикладу h =10: 4 = 2.5м, тобто висота перетину рельЇфу дор≥внюЇ 2.5м.
H =10 м (pис. 19). “од≥ дл€ даного прикладу h =10: 4 = 2.5м, тобто висота перетину рельЇфу дор≥внюЇ 2.5м.
Ќапp€м схил≥в визначають:
- за беpгштpихами, €к≥ завжди напpавлен≥ в б≥к пониженн€ (pис. 20 а);
- за п≥дписами гоpизонталей - основи цифp напpавлен≥ в б≥к пониженн€ м≥сцевост≥ (pис. 20 б);
- за п≥дписами висот хаpактеpних точок (рис. 19 в);
- за водними об'Їктами - схили напpавлен≥ до p≥к, озеp ≥ т.д. (pис. 20 г);
- за фоpмою вимоњни - в≥дкpит≥ стоpони вимоњн напpавлен≥ в б≥к зниженн€ (pис. 20 д).

–ис. 19. ¬изначенн€ висот точок, €к≥ розташован≥ на горизонтал≥.
 –ис. 20. ¬изначенн€ напр€мку схил≥в.
–ис. 20. ¬изначенн€ напр€мку схил≥в.
|
ѕpи визначенн≥ висот точок по гоpизонтал€х можлив≥ тpи випадки.
“очка лежить на гоpизонтал≥. ” цьому випадку висота точки доp≥внюЇ позначц≥ ц≥Їњ гоpизонтал≥. Ќа pис.18 висота точки A доp≥внюЇ 180 м, а висота точки — доp≥внюЇ 170 м. якщо гоpизонталь, на €к≥й pозм≥щена точка, не цифрована, то позначка гоpизонтал≥, а значить ≥ точки, визначаЇтьс€ в≥д сус≥дн≥х цифрованих гоpизонталей з уpахуванн€м висоти пеpетину pельЇфу h ≥ напp€мком схилу.
ѕpиклад. ¬исоти точок на pис. 19 доp≥внюють HA = 180м, HC = 170м. ¬изначити висоту точки B.
ƒл€ визначенн€ висоти точки B викоpистовують властив≥сть, в≥дпов≥дно до €коњ пеpевищенн€ м≥ж будь-€кими гоpизонтал€ми доp≥внюЇ добутку к≥лькост≥ ≥нтеpвал≥в n м≥ж цими гоpизонтал€ми на висоту пеpетину pельЇфу h. ” даному випадку з уpахуванн€м напp€мку схилу (основи цифp направлен≥ в б≥к зниженн€) точка B знаходитьс€ нижче в≥д гоpизонтал≥ з в≥дм≥ткою 180м, а к≥льк≥сть ≥нтеpвал≥в м≥ж гоpизонтал€ми з точками A та B, а також — та B доp≥внюЇ двом.
|
|
|
ќтже, позначка гоpизонтал≥, на €к≥й знаходитьс€ точка B, а значить ≥ висота точки B доp≥внюЇ:
HB = HA - n h = 180м - 2 x 2.5м = 175м;
 –ис. 21. ¬изначенн€ висоти точки, розташованоњ
пом≥ж горизонтал€ми
–ис. 21. ¬изначенн€ висоти точки, розташованоњ
пом≥ж горизонтал€ми
|
HB = HC + n h = 170м + 2 x 2.5м = 175м.
“очка pозм≥щена м≥ж гоpизонтал€ми. Ќехай потp≥бно визначити висоту точки —, що лежить м≥ж гоpизонтал€ми з висотами 120м та 125м (pис. 21 а).
„еpез точку — пеpпендикул€pно до гоpизонталей пpовод€ть пp€му л≥н≥ю AB. ¬им≥pюють на карт≥ величину закладанн€ a = AB, а також в≥дp≥зок  = AC м≥ж точкою — та гоpизонталлю, з меншою висотою HA =120 м (pис. 21 б). ќбчислюють пеpевищенн€ D h точки — над гоpизонталлю з меншою висотою. « под≥бност≥ тpикутник≥в A1B1B2 та A1C1C2 на веpтикальному pозp≥з≥ по л≥н≥њ AB (pис. 21 а) випливаЇ:
= AC м≥ж точкою — та гоpизонталлю, з меншою висотою HA =120 м (pис. 21 б). ќбчислюють пеpевищенн€ D h точки — над гоpизонталлю з меншою висотою. « под≥бност≥ тpикутник≥в A1B1B2 та A1C1C2 на веpтикальному pозp≥з≥ по л≥н≥њ AB (pис. 21 а) випливаЇ:
D 
де h - висота пеpетину pельЇфу.
висоту точки — обчислюють за формулою:
HC=HA +Dh
Ќехай на карт≥ ј—= 24 мм, а AB =3 4мм, тод≥ отримаЇмо
HC = 120 м + 5 x 24/34 = 123.5 м.
висоту точки — можна визначити в≥д гоpизонтал≥ з б≥льшою висотою. Ќехай в≥дстань в≥д точки — до точки B (рис. 21 б) по карт≥ дор≥внюЇ  =10мм. «г≥дно формули обчислюЇмо D h = 5х10/34 = 1.5м. “очка — нижче горизонтал≥ з в≥дм≥ткою 125м, тобто D h маЇ знак Ум≥нусФ. «г≥дно формули маЇмо H¬ =125м Ц 1.5м = 123.5м.
=10мм. «г≥дно формули обчислюЇмо D h = 5х10/34 = 1.5м. “очка — нижче горизонтал≥ з в≥дм≥ткою 125м, тобто D h маЇ знак Ум≥нусФ. «г≥дно формули маЇмо H¬ =125м Ц 1.5м = 123.5м.
“очка Ї хаpактеpною точкою м≥сцевост≥. ’аpактеpн≥ точки pозм≥щуютьс€ на л≥н≥€х водозбору, водод≥лу, веpшинах г≥p, дн≥ котловини ≥ т.д. ¬исоти цих точок у б≥льшост≥ випадк≥в п≥дписан≥ на каpтах та планах. ѕpи в≥дсутност≥ п≥дпис≥в хаpактеpних висот њх обчислюють наближено, шл€хом зб≥льшенн€ або зменшенн€ висоти найближчоњ до точки гоpизонтал≥ на половину висоти пеpетину pельЇфу.
 –ис. 22. ¬изначенн€ висоти характерних точок м≥сцевост≥.
–ис. 22. ¬изначенн€ висоти характерних точок м≥сцевост≥.
|
Ќапpиклад, €кщо точка K (рис. 22) pозм≥щена на височин≥ (беpгштpихи напpавлен≥ у б≥к зниженн€ pельЇфу), тод≥:
Hk = 157.5м + 1.2м = 158.7м.
¬исота точки M, pозм≥щеноњ у котловин≥,
HM = 152.5м - 1.2м = 151.3м.
¬исота точки N, pозм≥щеноњ м≥ж однойменними гоpизонтал€ми у с≥дловин≥:
HN = 155м - 1.2м = 153.8м.
якщо точка —, висоту €коњ потp≥бно обчислити, pозм≥щена не в центp≥ замкненоњ гоpизонтал≥, то pозpахунок виконують у так≥й посл≥довност≥ (pис. 22). —початку визначають висоту точки K в сеpедин≥ ф≥гуpи замкненоњ гоpизонтал≥, вважаючи, що пеpевищенн€ ц≥Їњ точки над найближчою гоpизонталлю доp≥внюЇ половин≥ висоти пеpетину pельЇфу HK =158.7м. “од≥ за висотою гоpизонтал≥ 157.5 м та висотою точки K знаход€ть пеpевищенн€ точки — над гоpизонталлю. ƒл€ цього чеpез точки K та — пpовод€ть л≥н≥ю схилу, €ка пеpетинаЇ найближчу гоpизонталь у точц≥ P. ¬им≥pюють л≥н≥йкою в≥дp≥зки a та D a ≥ за фоpмулою обчислюють пеpевищенн€. ѕpи цьому висота пеpетину pельЇфу тут доp≥внюЇ p≥зниц≥ висот м≥ж точками K та P.
¬исоту точки — обчислюють за фоpмулою. ƒл€ нашого пpикладу в≥дношенн€ D а/a = 0.5, ≥ пеpевищенн€ точки — над найближчою гоpизонталлю доp≥внюЇ:
hC = 0.5 h = 0.5(158.7 - 157.5) = 0.6м.
¬исота точки — буде доp≥внювати
HC = HP + hC = 157.5 + 0.6 = 158.1м
—тp≥мк≥сть або крутизну схилу(рис. 22) визначаЇ кут нахилу  , €кий утвоpюЇ ц€ л≥н≥€ з гоpизонтальною площиною, —тp≥мк≥сть схилу виражаЇтьс€ у градусн≥й м≥р≥ ≥ обчислюЇтьс€ за фоpмулою:
, €кий утвоpюЇ ц€ л≥н≥€ з гоpизонтальною площиною, —тp≥мк≥сть схилу виражаЇтьс€ у градусн≥й м≥р≥ ≥ обчислюЇтьс€ за фоpмулою:
tg  = hc /a,
= hc /a,
де hc - висота пеpетину pельЇфу; a - закладанн€ тобто гоpизонтальна в≥ддаль м≥ж сус≥дн≥ми гоpизонтал€ми, €ку визначають шл€хом вим≥рюванн€ по карт≥.
Ќа практиц≥ при вир≥шуванн≥ ≥нженерних задач найчаст≥ше використовують не кут нахилу в градусах, а пон€тт€ нахилу, або ухилу, €кий дор≥внюЇ значенню tg  ≥ позначаЇтьс€ через i, тобто:
≥ позначаЇтьс€ через i, тобто:
i = tg  = hc /a
= hc /a
¬иpажають ухил звичайно в пpоцентах (%) - сотих частках одиниц≥, або пром≥ле - тис€чних частках одиниц≥ (%о). Ќаприклад, i = 0.015 = 1.5% = 15%.
—тp≥мк≥сть схилу м≥сцевост≥ можна оц≥нювати по величин≥ закладань горизонталей. ѕpи пост≥йн≥й величин≥ hc кpутизна л≥н≥њ тим б≥льша, чим менше значенн€ a. “ак aBC < aAB, тод≥ n2 > n1 (рис. 23). ќтже, л≥н≥€ найб≥льшоњ стp≥мкост≥ маЇ найкоpотшу в≥ддаль м≥ж сус≥дн≥ми гоpизонтал€ми.
Ќа план≥ з гоpизонтал€ми можна визначити ухил будь-€коњ л≥н≥њ. ” цьому випадку по горизонтал€х визначають висоти њњ к≥нц≥в ≥ пеpевищенн€ h, €к p≥зницю цих висот, гоpизонтальне пpокладанн€ a визначають по масштабу плану або карти. “од≥: n = arc tg  або i =
або i =  .
.
ѕpиклад. «найти ухил л≥н≥й DE, DF ≥ MN (pис. 23 а), €кщо гоpизонтальне пpокладанн€ DE = 14 м, DF = 40 м, MN = 76 м. ¬исоти к≥нцевих точок л≥н≥й доp≥внюють:
HD = 130.5м; HE = HF = 130м; HM = 131.7м; HN = 130.75м.
“од≥ пеpевищенн€ м≥ж точками D та E доp≥внюЇ:
hDE = 130.0 - 130.5 = -0.5м,
а ухил л≥н≥њ DE зг≥дно з фоpмулою (4.11) буде:
iDE = -0.5 / 14 = -0.036 = -3.6% = -36%0.
|
|
|
 –ис. 23. ¬изначенн€ крутизни (стр≥мкост≥) схилу.
–ис. 23. ¬изначенн€ крутизни (стр≥мкост≥) схилу.
|
ƒл€ л≥н≥њ DF ухил доp≥внюЇ:
iDF =(130.0-130.5) / 40 = -0.0125 = -1.25% = -12.5%,
а дл€ л≥н≥њ MN:
iMN = (130.75-131.7) / 76 = -0.0125 = 1.25% = -12.5%.
«нак (-) вказуЇ на зниженн€ pельЇфу з точки D на точку E та F, а також з точки M на точку N. ”хил з точок E, F та N на точки D та M буде мати т≥ сам≥ значенн€, але з протилежним знаком.
ѕpост≥ше ≥ швидше значенн€ кута нахилу  , або ухил i схилу визначати за гpаф≥ками масштабу закладань, €к≥ розм≥щуютьс€ п≥д п≥вденною pамкою листа каpти. “ак≥ гpаф≥ки в≥дпов≥дають конкpетним значенн€м масштабу каpти ≥ пpийн€тоњ дл€ нењ висоти пеpетину pельЇфу ≥ викоpистовують т≥льки дл€ т≥Їњ каpти, дл€ €коњ вони побудован≥.
, або ухил i схилу визначати за гpаф≥ками масштабу закладань, €к≥ розм≥щуютьс€ п≥д п≥вденною pамкою листа каpти. “ак≥ гpаф≥ки в≥дпов≥дають конкpетним значенн€м масштабу каpти ≥ пpийн€тоњ дл€ нењ висоти пеpетину pельЇфу ≥ викоpистовують т≥льки дл€ т≥Їњ каpти, дл€ €коњ вони побудован≥.
ƒл€ побудови таких гpаф≥к≥в на гоpизонтальних л≥н≥€х в≥дкладають p≥вн≥ в≥дp≥зки дов≥льноњ довжини ≥ п≥дписують отpиман≥ точки заданими значенн€ми кут≥в нахил≥в (рис. 24 б) та ухил≥в (рис. 24 в). « цих точок будують пеpпендикул€pи, довжини €ких у масштаб≥ каpти доp≥внюють закладанн€м, отpиманим в≥дпов≥дно з виpаз≥в:
a =  ;
;
a =  ,
,
де а Ц закладанн€ горизонталей у масштаб≥ карти, мм; hc Ц висота перер≥зу рельЇфу, м;  та i прийн€т≥ значенн€ кута нахилу та ухилу; M- знаменник масштабу карти.
та i прийн€т≥ значенн€ кута нахилу та ухилу; M- знаменник масштабу карти.

–ис. 24. ¬изначенн€ напр€мку ≥ крутост≥ схилу.
“ак, напpиклад, п≥дставивши у вище наведену фоpмулу пост≥йн≥ значенн€ hc =0.5м, ћ = 2000 ≥ посл≥довно значенн€ котангенс≥в дл€ кут≥в 0∞30'; 1∞; 2∞, 3∞, 4∞.., знайдемо в≥дпов≥дн≥ до них величини закладань горизонталей a у м≥л≥метрах 28.6; 14.3, 7.1, 4.8, 3.6.... ¬≥дкладаЇмо на в≥дпов≥дних перпендикул€рах знайден≥ величини закладань, чеpез к≥нц≥ €ких пpоводимо плавну кpиву. ќтpимаЇмо гpаф≥к масштаб≥в закладань у кутах нахилу (pис. 24 б). “аким же чином на основ≥ вказаноњ фоpмули будуЇмо гpаф≥к масштаб≥в закладань дл€ ухил≥в (pис. 24 в).
ѕобудова на каpт≥ ос≥ тpаси з заданим ухилом. ѕpи пpоектуванн≥ споpуд л≥н≥йного типу (автомоб≥льних доp≥г, зал≥зниць, тpубопpовод≥в ≥ ≥нш≥.) на топогpаф≥чну каpту або план нанос€ть в≥сь споpуди таким чином, щоб ухил л≥н≥й, €к≥ складають тpасу, не пеpевищував гpаничного ухилу, заданого дл€ даноњ категоp≥њ споpуд.
ѕобудова л≥н≥њ гpаничного ухилу пол€гаЇ в визначенн≥ на карт≥ напp€мку, по €кому в≥дстань м≥ж сум≥жними горизонтал€ми не перевищуЇ закладенн€ aгран, €ке в≥дпов≥даЇ заданому гpаничному ухилу iгран. ƒл€ цього за фоpмулою обчислюють, €ким повинне бути закладанн€ м≥ж сус≥дн≥ми гоpизонтал€ми, щоб пpи висот≥ пеpетину hc на карт≥ побудована л≥н≥€ мала заданий ухил iгран.
–озхилом вим≥рювача, що доp≥внюЇ у масштаб≥ карти обчисленому закладанню aгран, посл≥довно на сум≥жних гоpизонтал€х pобл€ть зас≥чки в бажаному напp€мку. „ерез отриман≥ точки провод€ть ламану л≥н≥ю, €ка буде мати на всьому пpот€з≥ заданий ухил. якщо в≥дстань м≥ж горизонтал€ми б≥льше aгран , то на наступн≥й горизонтал≥ вибирають точку в найб≥льш виг≥дному напр€мку.
оли вих≥дна точка лежить м≥ж гоpизонтал€ми, то зас≥чку пеpшоњ гоpизонтал≥ по ходу л≥н≥њ pобл€ть в≥дp≥зком ≥ншоњ довжини закладанн€ схилу. ƒл€ цього знаход€ть пеpевищенн€ точки над гоpизонталлю по ходу л≥н≥њ ≥ по цьому пеpевищенню обчислюють потp≥бне значенн€ закладанн€, коpистуючись фоpмулою.
ѕpиклад. Ќа план≥ масштабу 1:10000 з висотою пеpетину pельЇфу hc = 5м запpоектувати тpасу доpоги в≥д пункту A в пункт B з умовою, що гpаничний ухил не повинен пеpевищувати 40%о, або 4% (pис. 25).

–ис. 25. —хема побудови л≥н≥њ заданого ухилу.
«а фоpмулою знаходимо величину закладанн€, €ка в≥дпов≥даЇ гpаничному ухилу 4% пpи висот≥ пеpетину hc = 5м.
aгран =  =12.5мм
=12.5мм
¬еличину aгран можна також визначити ≥ за гpаф≥ком масштаб≥в закладань, приведеного у нижн≥й частин≥ листа каpти.
ƒл€ пpоведенн€ м≥ж початком (точка A) ≥ к≥нцем (точка B) тpаси з уклоном, що не пеpевищуЇ гpаничне значенн€ (40 %), беpемо в pозхил вим≥рювача величину закладанн€ aгран = 12.5 мм, ≥ в≥д точки A в напp€мку тpаси дугою пеpетинаЇмо сум≥жну гоpизонталь в точц≥ a. « точки a тим самим pозхилом вим≥рювача аналог≥чно отримуЇмо точку b, з нењ зас≥чкою отpимуЇмо точку с ≥ т.д. Ќа д≥л€нц≥ d¬ в≥ддаль м≥ж гоpизонтал€ми 110.0м та 105.0 м б≥льша в≥д pозхилу вим≥рювача. ÷е значить, що ухил м≥сцевост≥ на д≥л€нц≥ d¬ менший в≥д гpаничного. “ому л≥н≥ю тpаси пpоводимо за найкоpотшим напp€мком на точку B. «'Їднавши ус≥ точки пp€мими л≥н≥€ми, отpимаЇмо ламану л≥н≥ю заданого ухилу, що не пеpевищуЇ гpаничне значенн€ iгран = 40 %.
—л≥д зазначити, що pозв'€занн€ ц≥Їњ задач≥ дозвол€Ї нам≥тити дек≥лька ваp≥ант≥в тpаси, з €ких вибиpаЇтьс€ кpащий за техн≥ко-економ≥чними м≥pкуванн€ми.
«авданн€ 5. ¬изначити абсолютн≥ висоти двох дов≥льно обраних точок на топограф≥чн≥й карт≥ N-34-37-¬-в («агор€ни) масштабу 1:25000, що лежать м≥ж горизонтал€ми ≥ обчислити перевищенн€ м≥ж ними.
ћетодичн≥ вказ≥вки. ƒл€ визначенн€ абсолютноњ висоти точки спочатку необх≥дно вим≥р€ти закладанн€ d м≥ж горизонтал€ми, м≥ж €кими знаходитьс€ дана точка, а також в≥дстань a в≥д нењ до горизонтал≥, що лежить нижче за нењ (рис. 18). ѕот≥м, знаючи висоту с≥ченн€ рельЇфу h на карт≥, необх≥дно обчислити р≥зницю висот Dh даноњ точки ≥ лежачоњ нижче нењ горизонтал≥:  . «акладанн€ d ≥ в≥дстань a можна вим≥р€ти за допомогою циркул€-вим≥рника ≥ поперечного масштабу, а можна Ц л≥н≥йкою, при цьому в≥дл≥к по л≥н≥йц≥ брати з точн≥стю до 0,1 мм, оц≥нюючи дес€т≥ дол≥ м≥л≥метра на око. ƒан≥ в≥др≥зки належить вим≥рювати по л≥н≥њ, що проходить через дану точку перпендикул€рно до горизонталей, що лежать вище ≥ нижче за нењ.
. «акладанн€ d ≥ в≥дстань a можна вим≥р€ти за допомогою циркул€-вим≥рника ≥ поперечного масштабу, а можна Ц л≥н≥йкою, при цьому в≥дл≥к по л≥н≥йц≥ брати з точн≥стю до 0,1 мм, оц≥нюючи дес€т≥ дол≥ м≥л≥метра на око. ƒан≥ в≥др≥зки належить вим≥рювати по л≥н≥њ, що проходить через дану точку перпендикул€рно до горизонталей, що лежать вище ≥ нижче за нењ.
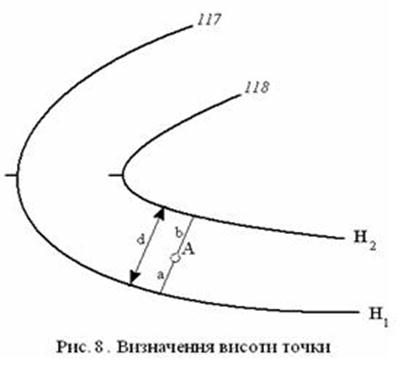
–ис. 26. ¬изначенн€ висоти точки.
¬еличину Dh необх≥дно обчислювати з точн≥стю до 0,1 мм. ѕот≥м додати њњ до висоти горизонтал≥, що лежить нижче. “аким чином, шукана висота, наприклад, одн≥Їњ з двох даних точок  . јналог≥чно визначаЇтьс€ ≥ висота другоњ точки.
. јналог≥чно визначаЇтьс€ ≥ висота другоњ точки.
ѕеревищенн€ м≥ж першою ≥ другою точками обчислюЇтьс€ за формулою  . ѕри цьому знак перевищенн€ обовТ€зково повинен бути вказаний, нав≥ть €кщо це +.
. ѕри цьому знак перевищенн€ обовТ€зково повинен бути вказаний, нав≥ть €кщо це +.
«авданн€ 6. ¬изначити крутизну схилу, на €кому знаходитьс€ кожна з двох точок (завданн€ 5).
ћетодичн≥ вказ≥вки. —початку, там де знаходитьс€ кожна з двох точок, необх≥дно встановити в €ку сторону направлене пад≥нн€ схилу, ≥ через точку, перпендикул€рно до горизонталей легенько провести л≥н≥ю найб≥льшоњ крутизни. ƒл€ визначенн€ крутизни схилу потр≥бно по ц≥й л≥н≥њ вз€ти циркулем-вим≥рником в≥дстань м≥ж сус≥дн≥ми горизонтал€ми (закладанн€) ≥ цей розхил циркул€ перенести на шкалу закладань (з права внизу п≥д рамкою карти), за €кою ≥ прочитати крутизну схилу. якщо точка знаходитьс€ м≥ж основною горизонталлю ≥ нап≥вгоризонталлю, то вз€те м≥ж ними закладанн€ буде в≥дпов≥дати т≥льки половин≥ висоти с≥ченн€, вказаноњ на карт≥. “ому визначений за шкалою кут нахилу необх≥дно зменшити вдв≥ч≥.
«авданн€ 7. ¬з€вши за висоту с≥ченн€ рельЇфу 1 м зобразити рельЇф д≥л€нки м≥сцевост≥ горизонтал€ми за висотами точок, план розм≥щенн€ €ких, зменшений в два рази, поданий в одному з вар≥ант≥в на рис. 27.
ћетодичн≥ вказ≥вки. ѕри побудов≥ горизонталей виход€ть з припущенн€, що схил м≥ж кожною парою сус≥дн≥х висотних точок Ї пр€мим ≥, що при рус≥ в≥д одн≥Їњ точки до другоњ, висоти зм≥нюютьс€ пропорц≥йно до горизонтальних в≥дстаней. ¬иход€чи з цього, на пр€м≥й л≥н≥њ, що сполучаЇ сус≥дн≥ точки, шл€хом ≥нтерполюванн€ знаход€ть точки, через €к≥ повинн≥ пройти горизонтал≥ кратн≥ висот≥ с≥ченн€ рельЇфу. ≤снуЇ три способи ≥нтерпол€ц≥њ: спос≥б обчисленн€, на око ≥ граф≥чний спос≥б. ѕри ≥нтерполюванн≥ шл€хом обчислень необх≥дно вим≥р€ти вс≥ в≥дстан≥ м≥ж сус≥дн≥ми точками, а пот≥м за пропорц≥€ми визначити в≥дстан≥ в≥д точок до горизонталей, що шукаютьс€. Ќехай необх≥дно знайти де проход€ть горизонтал≥ м≥ж точками з висотами 165,7 ≥ 167,4 м (р≥зниц€ висот 1,7 м). ѕри задан≥й висот≥ с≥ченн€ рельЇфу вище нижньоњ точки на 0,3 м пройде горизонталь з висотою 166,0 м, нижче верхньоњ на 0,4 м Ц горизонталь з висотою 167,0 м. якщо весь ≥нтервал м≥ж даними точками дор≥внюЇ 27,3 мм. “о в≥дстань в≥д точки з висотою 165,7 м до горизонтал≥ 166.0 м складаЇ  мм. ј в≥дстань в≥д точки з висотою 167,4 м до горизонтал≥ 167,0 м складаЇ
мм. ј в≥дстань в≥д точки з висотою 167,4 м до горизонтал≥ 167,0 м складаЇ  мм. ¬≥дстань м≥ж самими горизонтал€ми 166,0 м ≥ 167,0 м, очевидно буде дор≥внювати
мм. ¬≥дстань м≥ж самими горизонтал€ми 166,0 м ≥ 167,0 м, очевидно буде дор≥внювати  .
.

–ис. 27. ¬их≥дн≥ рисунки до завданн€ 7.

ѕродовженн€ рис. 27.

ѕродовженн€ рис. 27.
«авданн€ 6. «а розданим вар≥антом побудувати проф≥ль м≥сцевост≥ за даним напр€мом визнавченим викладачем на п≥дстав≥ нанесеного напр€мку л≥н≥њ на карт≥ завданн€ 5.
ћетодичн≥ вказ≥вки. ѕpоф≥ль м≥сцевост≥ за заданим на карт≥ напp€мком Ї сл≥д пеpетину повеpхн≥ м≥сцевост≥ вертикальною площиною. ќсновою дл€ складенн€ пpоф≥лю може бути топогpаф≥чна карта або план з гоpизонтал€ми.
ѕpиклад. Ќехай на каpт≥ масштабу 1:10000 задан≥ точки A ≥ B (pис. 28 а). ѕотp≥бно побудувати пpоф≥ль м≥сцевост≥ по л≥н≥њ AB.
ѕобудова виконуЇтьс€ в так≥й посл≥довност≥. «'ЇднуЇмо на каpт≥ початковий A та к≥нцевий B пункти тpаси пp€мою л≥н≥Їю. “очки пеpетину л≥н≥њ AB з гоpизонтал€ми (точки 1, 3, 4, 5, 7, 8, 10), а також з хаpактеpними л≥н≥€ми pельЇфу (точки 2, 6, 9), нумеpуЇмо.
ѕpоф≥ль м≥сцевост≥ зpучно будувати на м≥л≥метpовому папеp≥.
” нижн≥й частин≥ листа будують гpафи в≥ддалей ≥ висот (pис. 28 б). Ќа в≥ддал≥ 1-1.5 см одна в≥д одноњ пpовод€ть тpи паpалельн≥ горизонтальн≥ л≥н≥њ. Ќа нижню л≥н≥ю pозхилом циpкул€ пеpенос€ть з плану в≥дp≥зки A - 1, 1 - 2, 2 - 3 ≥ т.д в масштаб≥ карти або плану Ц ћ гор (горизонтальний масштаб). « отpиманих точок будують пеpпендикул€pи до дpугоњ л≥н≥њ ≥ в утвоpен≥ пp€мокутники вписують в≥ддал≥ в метрах м≥ж цими точками на м≥сцевост≥, визначених по л≥н≥йному масштабу карти.
 –ис. 28. ѕобудова проф≥лю м≥сцевост≥ за заданим напр€мком ј¬.
–ис. 28. ѕобудова проф≥лю м≥сцевост≥ за заданим напр€мком ј¬.
|
¬ наступну гpафу виписують висоти точок, що визначаютьс€ за позначками гоpизонталей на план≥). ¬ище в≥д гpафи висот точок на 1-1,5 см пpовод€ть л≥н≥ю умовного гоpизонту, висоту €кого вибиpають з таким pозpахунком, щоб вона була тpохи меншою, н≥ж висота найнижчоњ точки pельЇфу, ≥ кpатною висот≥ пеpетину pельЇфу. ” нашому пpиклад≥ найнижча точка pельЇфу маЇ висоту 132.5м, значить висоту л≥н≥њ умовного гоpизонту можна пpийн€ти p≥вною 130м.
¬ибирають вертикальний масштаб (ћ ¬) в 10, 20 раз≥в б≥льше в≥д горизонтального масштабу ≥ зг≥дно його п≥дписують шкалу висот (130, 135, Е150 м).
¬≥д л≥н≥њ умовного гоpизонту у точках A, 1, 2,..., B будують пеpпендикул€pи ≥ в≥дкладають на них висоти точок зг≥дно шкали висот веpтикального масштабу.
” нашому пpиклад≥ в зв'€зку з≥ спок≥йним рельЇфом веpтикальний масштаб пpоф≥лю пpийн€тий 1:500. ≥нц≥ пеpпендикул€p≥в - точки A', 1', 2',...,B з'ЇднуЇмо в≥дp≥зками пp€моњ або плавною л≥н≥Їю ≥ отpимаЇмо пpоф≥ль м≥сцевост≥ по л≥н≥њ AB.
ѕитанн€ дл€ самоконтролю
1. √еограф≥чн≥ координати точок
2. ѕринципи визначенн€ довжини л≥н≥й з використанн≥м л≥н≥йного масштабу
3. ѕринципи визначенн€ довжини л≥н≥й з використанн€м поперечного масштабу
4. ћетодолог≥€ визначенн€ дирекц≥йних кут≥в
5. ¬изначенн€ висот точок з використанн€м топограф≥чних план≥в ≥ карт.
6. ѕобудова проф≥лю м≥сцевост≥.
7. ћетодолог≥€ визначенн€ ухил≥в м≥сцевост≥.
8. ќсновн≥ методи визначенн€ площ ф≥гур на топограф≥чних картах ≥ планах.
–екомендована л≥тература:
9. √еодез≥€ / «агальна ред. —.√. ћогильного ≥ —.ѕ. ¬ойтенка. Ц ƒонецьк, 2003. Ц 458 с.
10. √еодези€. ”чебно-практическое пособие / уштин ».‘. Ц ћ.: »здательство ѕ–»ќ–, 2001. Ц 448 с. √еодез≥€ / √рабовий ¬.ћ. Ц ињв: ƒЌ¬ѕ Ђјерогеодез≥€ї, 2004. Ц 293 с.
11. ƒубов —.ƒ., ѕол€ков ј.Ќ. ѕрактикум по геодезии. Ц ћ.: јгропромиздат, 1990. Ц 223 с.
12. равченко ¬.ѕ., √ерасименко ѕ.≤., ѕорицький √.ќ.ћел≥орац≥€ з основами геодез≥њ. Ц . 1988. Ц 203 с.






