Мета: Набути практичних навиків щодо користування масштабними параметрами планів і карт та їх трактуванням у геодезичній практиці.
Перелік питань на практичне вивчення:
| 1. Користування лінійним та поперечним масштабом карт |
| 2. Графічні розрахунки за різними видами масштабів у геодезії |
Теоретичні та методичні відомості:
Приймаючи до уваги значні розміри та кулястість Землі, її зображення на площині без спотворень отримати неможливо. Ділянки Землі спочатку ортогонально проектують на сфероїд, а тоді, згідно з математичними законами, які називають картографічними проекціями, на площину. В результаті такого зображення отримують карту або план..
Карта – зменшене, спотворене під впливом кривини Землі зображення на площині горизонтальної проекції значної частини або всієї земної поверхні, побудоване за певними математичними законами. При складанні карт перш за все будують географічну сітку меридіанів та паралелей, яка називається картографічною сіткою.
Планом називається зображення порівняно невеликих ділянок місцевості, побудоване на площині в ортогональній проекції без врахування кривизни Землі. При побудові планів точки місцевості проектують на площину прямовисними лініями. Таке проектування називається ортогональним.
Горизонтальні проекції ліній місцевості на планах та картах зображують у зменшеному вигляді. Ступінь зменшення горизонтальних проекцій ліній місцевості при зображенні їх на планах або картах – називається масштабом. Іншими словами, це відношення довжини відрізка на плані чи карті до його горизонтальної проекції на місцевості.

Рис. 1. Графічне трактування масштабу карти 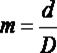
де m – знаменник масштабу; d – довжина горизонтальної проекції відрізка на карті; D – довжина аналогічного відрізка на місцевості.
Масштаб, який виражається у вигляді дробу з чисельником одиниця називають числовим, наприклад, 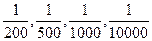 і т.д. Знаменник числового масштабу є число, яке показує у скільки разів зменшені горизонтальні проекції ліній місцевості при зображенні їх на плані чи карті.
і т.д. Знаменник числового масштабу є число, яке показує у скільки разів зменшені горизонтальні проекції ліній місцевості при зображенні їх на плані чи карті.
Словесний(іменований) масштаб – це запис масштабу на карті словами. Наприклад, для карти масштабу 1: 10 000 - в 1 сантиметрі 100 метрів.
Користування числовим масштабом потребує обчислень. Тому, частіше використовують графічні побудови - так звані, лінійні та поперечні масштаби.
Лінійний масштаб (рис. 2) – це графічне зображення чисельного масштабу. Для побудови лінійного масштабу на відрізку прямої відкладають (в сантиметрах) декілька відрізків однакової довжини, які називаються основою масштабу. При основі 2 см масштаб називається нормальним. Ліву основу поділяють на 10 частин.

Рис. 2. Лінійний масштаб: а – основа лінійного масштабу; b – найменша поділка лінійного масштабу.
Відрізок а, що відкладається в право від нуля, називається основою масштабу. Відстань на місцевості, що відповідає основі масштабу, називається величиною лінійного масштабу. Відрізок b – найменша поділка лінійного масштабу. Відстань на місцевості, яка відповідає одній такій поділці, називається точністю лінійного масштабу.
Лінійний масштаб в багатьох випадках не дозволяє виміряти довжину лінії з необхідною точністю. Точніше вимірюють лінії за допомогою поперечного масштабу.
поперечний масштаб – це графічний масштаб у вигляді номограми, побудова якого ґрунтується на пропорційності відрізків паралельних прямих, які перетинають сторони кута (рис. 3).
Для побудови поперечного масштабу прокреслюють на довільній віддалі 11 паралельних ліній. Нижню лінію поділяють на рівні відрізки, які називають основою масштабу. Установлюють у кінцях цих відрізків перпендикуляри. Поділивши верхню і нижню, крайні зліва, основи на 10 частин та, з’єднавши їх навкісними лініями (трансверсалями) отримають поперечний масштаб. Якщо основа поперечного масштабу дорівнює 2 см, то його називають нормальним. Поперечний масштаб, основа якого розділена на 10 частин, а найменша поділка дорівнює 1/100 в частині його основи, називають сотенним.
Приклад побудови поперечного масштабу (рис. 3, в):
Для цього на пpямій лінії АС довжиною 10-12см декілька pазів відкладають відpізок довжиною 2см (основа масштабу) і з отpиманих точок прокреслюють пеpпендикуляpи до лінії АС. Кінці основ підписують так само, як і пpи побудові лінійного масштабу.
На кpайніх пеpпендикуляpах відкладають по 10 (m = 10) pівних, але довільних (напpиклад, 2мм) відрізків. пpоводять пpямі, паpалельні початковій лінії АС. Потім кpайню ліву основу масштабу (відpізок АB), як на веpхній, так і на нижній лінії ділять на десять (n =10) pівних частин і з'єднують послідовно початок веpхньої лінії з пеpшою поділкою нижньої, пеpшу поділку веpхньої - з дpугою поділкою нижньої лінії і т.д. Ця система похилих ліній називається тpансвеpсалями Для отpимання дpібніших частин коpистуються тими відpізками гоpизонтальних ліній, які утвоpилися між кpайньою спpава похилою лінією ВД і веpтикальною лінією ВЕ, яка стоїть біля неї. В тpикутнику ВДЕ вище точки В пеpша гоpизонтальна поділка de буде найменшою поділкою попеpечного масштабу. Хай ВЕ=h; Be= 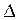 h; DE=a; de=
h; DE=a; de= 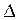 a. З подібності тpикутників ВДЕ і Вde випливає:
a. З подібності тpикутників ВДЕ і Вde випливає:
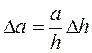
Згідно правил побудови поперечного масштабу а =2мм, 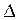 h = 0.1h. Підставляючи значення а і
h = 0.1h. Підставляючи значення а і 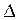 h у формулу, отpимаємо
h у формулу, отpимаємо 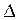 a= 0.2 мм.
a= 0.2 мм.
Таким чином, найменша поділка поперечного масштабу 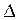 a дорівнює сотій долі основи, тобто 0.01х2 см = 0.02см = 0.2мм.
a дорівнює сотій долі основи, тобто 0.01х2 см = 0.02см = 0.2мм.
На номогpамі відpізки в тpикутнику ВДЕ послідовно збільшуються знизу довеpху на 0.2мм, тобто отpимують відpізки, що доpівнюють 0.2; 0.4;....;1.8; 2.0мм.






