В теории и технике сигналов широко используется теорема Котельникова (теорема отсчетов): если наивысшая частота в спектре функции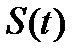 
меньше, чем 
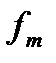, то функция 
полностью определяется последовательностью значений в момент времени, отстоящие друг от друга не больше чем на 
секунд.
В соответствии с этой теоремой сигнал ограниченный по спектру наивысшей частотой 
, можно представить рядом
(3.1)
В этом выражении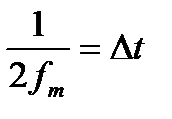 
обозначает интервал между двумя отсчетными точками на оси времени, а 
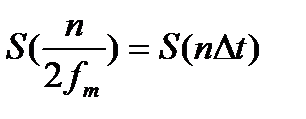-выборка функции в момент времени 
.
Представление функции рядом иллюстрирует рис.3.10:
рис.3.1
Функция вида
(3.2)
обладает следующими свойствами:
1. в точке 
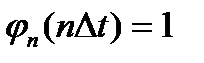, а в точках 
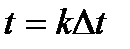, где 
- любое целое положительное или отрицательное число, отличное от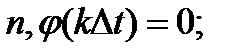 
2. спектральная плотность функции 
равномерна в полосе частот 
и равна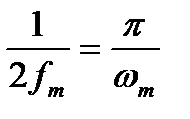 
.
Так как функция отличается от 
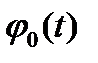только сдвигом на оси времени на 
, то спектральная плотность функции
(3.3)
Ряд (3.1) точно определяет заданный сигнал в точках отсчета, поскольку коэффициенты ряда есть сами выборки из функции, т.е. величины 
.
Рассмотрим случай когда длительность сигнала конечна и равна 
, а полоса частот равна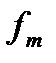 
. При этом случае и определенных допущениях общее число независимых параметров (т.е. значений 
), которое необходимо для полного задания сигнала, очевидно будет 
При этом выражении (3.1) принимает вид (при отсчете времени от первой выборки):
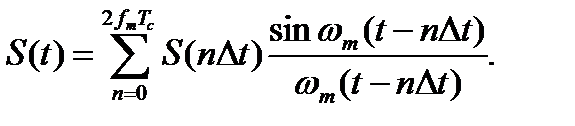
(3.4)
Число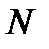 
иногда называют числом степеней свободы сигнала , а иногда и базой сигнала.
Энергию и среднюю мощность сигнала нетрудно выразить через заданную последовательность временных выборок.
Средняя за время мощность непрерывного сигнала равна среднему квадрату выборки, число которых равно 
.
