Дискретный сигнал 
с точностью до коэффициента пропорциональности 
равен произведению функции 
и дискретизирующей последовательности 
:
(3.6)
Известно, что спектр произведения двух сигналов пропорционален свертке их спектральных плотностей. Поэтому если известны законы соответствия сигналов и спектров:
то спектральная плотность дискретизированного сигнала
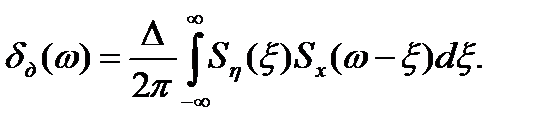
(3.7)
Чтобы найти спектральную плотность дискретизирующей последовательности, разложим периодическую функцию в комплексный ряд Фурье:
Коэффициенты этого ряда 
Исходя из фильтрующих свойств дельта функции получаем
(3.8)
т.е. спектр дискретизирующей последовательности состоит из бесконечной совокупности дельта-импульсов в частной области. Данная спектральная плотность является периодической функцией с периодом 
Подставим формулу (3.8) в (3.7) и изменив порядок следования операций интегрирования и суммирования, находим
(3.9)
Спектр сигнала, полученного в результате дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа “копий” спектра исходного аналогового сигнала. Копии располагаются на оси частот через одинаковые интервалы 
, равные значению угловой частоты первой гармоники дискретизирующей импульсной последовательности.
рис.3.3
