Пусть задан импульс 
и соответствующая ему спектральная плотность 
(рис.2а)
а)
б)
рис2.2
На рисунке изображен модуль сплошного спектра 
в виде функции, четной относительно 
При повторении импульсов с периодом 
получается последовательность, представленная на рис. 2.2,б (слева). Линейчатый (дискретный) спектр этой последовательности изображен в правой части рисунка. При периоде интервал между любыми двумя соседними гармониками равен 
.
Коэффициент 
- й гармоники
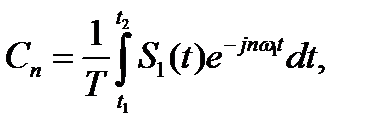
где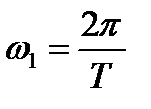 
, 
и 
соответствуют рис.2.1.
Спектральная плотность одиночного импульса на той же частоте 
исходя из (2.6) будет
Спектральная плотность 
отличается от коэффициента 
ряда Фурье периодической последовательности только отсутствием множителя 
.
Следовательно имеет место простое соотношение
(2.13)
Соответственно комплексная амплитуда 
- й гармоники
(2.13’)
Итак, модуль спектральной плотности одиночного импульса и огибающая линейчатого спектра периодической последовательности, полученной путем повторения заданного импульса, совпадает по форме и отличаются только масштабом.
На рис. (2.2,б) штриховой линией обозначена огибающая линейчатого спектра 
С увеличением спектральные линии на рис. (2.2,б) сближаются и коэффициенты уменьшаются, но так, что отношение 
остается неизменным. В пределе, при 
, приходим к одиночному импульсу со спектральной плотностью.
Таким образом становится наглядным термин “спектральная плотность”: 
есть амплитуда напряжения(тока), приходящаяся на 1 Гц в бесконечно узкой полосе частот, которая включает в себя рассматриваемую частоту 
.
