Гармонический анализ периодических сигналов. Свойства преобразования Фурье
2.1 Гармонический анализ непериодических сигналов.
Гармонический анализ периодических сигналов можно распространить на непериодические сигналы. Пусть такой сигнал 
задан в виде некоторой функции, отличной от нуля в промежутке 
.
(рис. 2.1)
Выделив произвольный отрезок времени 
, включающий в себя промежуток , мы можем представить заданный сигнал в виде ряда Фурье
(2.1)
где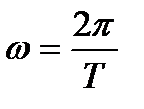 
, а коэффициенты 
в соответствии с формулой (1.14)
(2.2)
Подставив (2.2) в (2.1), получим
(2.3)
здесь учтено, что 
Вне отрезка 
ряд (2.1) определяет функцию 
0, где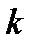 
- целое число, т.е. периодическую функцию, полученную повторением вправо и влево с периодом 
. Для того чтобы вне отрезка 
функция равнялась нулю, величина 
должна быть бесконечно большой. Но чем больше отрезок , выбранный в качестве периода, тем меньше коэффициенты . Устремляя к бесконечности, в пределе получаем бесконечно малые амплитуды гармонических составляющий, сумма которых изображает исходную непериодическую функцию , заданную в интервале 
(рис.2.1). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, т.к. при 
основная частота функции 
. Иными словами, расстояние между спектральными линиями, равно основной частоте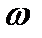 
становится бесконечно малым, а спектр – сплошным.
Поэтому в выражении (2.3) можно заменить 
на 
, на текущую частоту , а операции суммирования операцией интегрирования.
Таким образом, приходим к двойному интегралу Фурье
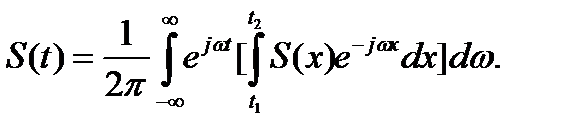
(2.4)
Внутренний интеграл, являющейся функцией ,
(2.5)
называется спектральной плотностью или спектральной характеристикой функции .
В случае, когда пределы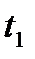 
и 
не уточнены, спектральная плотность записывается в форме
(2.6)
После подстановки (2.6) в (2.4) получаем
(2.7)
Выражения (2.6) (2.7) называются прямым и обратным преобразованием Фурье.
Выражение (2.6) отличается от (1.14) отсутствием множителя 
. Следовательно, спектральная плотность 
обладает всеми основными свойствами коэффициентов комплексного ряда Фурье.
По аналогии с (1.15) можно написать
(2.8)
где
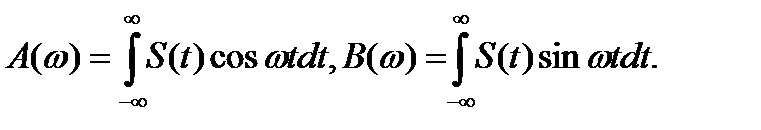
(2.9)
Модуль и аргумент спектральной плотности определяется выражениями
(2.10)
(2.11)
Первое из этих выражений можно рассматривать как АЧХ, а втрое как ФЧК сплошного спектра непериодического сигнала .
На основании (2.8) нетрудно привести интегральные преобразование (2.7) к тригонометрической форме. Имеем, аргумент функции 
в последующих выражениях опущен:
Из четности модуля и нечетности фазы следует, что подинтегральная функция в первом интеграле является четной, а во втором- нечетной относительно 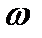. Следовательно, второй интеграл равен нулю и окончательно:
(2.12)
Отметим, что при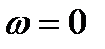 
выражение (2.5) переходит в следующее:
площадь под кривой .
(2.12)
Следовательно для любого сигнала спектральная плотность 
на первой частоте равна “площади сигнала”. Это правило полезно для быстрого выявления структуры спектра некоторых сигналов.
