Опыт конструирования САУ показал, что составляющие их звенья различной физической природы, имеющие различное конструктивное исполнение, могут иметь идентичный характер поведения, а значит, описываться идентичными частотными и временными функциями.
С этой точки зрения все звенья в системах автоматического управления можно разбить по характеру происходящих в них процессов на несколько типов. Тип звена однозначно определяется законом, связывающим между собой сигналы на его входе 
и выходе y (t).
Усилительное звено изменяет величину передаваемого сигнала, не преобразуя характер его изменения во времени. Уравнение и передаточная функция звена имеют соответственно следующий вид:
, (1.21)
, (1.22)
где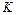 
– коэффициент усиления (передачи), который может принимать как положительное, так и отрицательное действительное значение.
Звено с запаздыванием осуществляет операцию сдвига входного сигнала на время 
в прошлое. Уравнение и передаточная функция звена имеют соответственно следующий вид:
, (1.23)
, (1.24)
где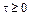 
– время запаздывания.
Идеальное дифференцирующее звено формирует на выходе сигнал, пропорциональный производной от входного сигнала. Уравнение и передаточная функция звена имеют соответственно следующий вид:
, (1.25)
, (1.26)
где 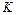– коэффициент усиления.
Передаточная функция реального дифференцирующего звена записывается, как
, (1.27)
где 
– коэффициент усиления;
– постоянная времени.
Интегрирующее звено формирует на выходе сигнал, пропорциональный интегралу от входного сигнала. Уравнение и передаточная функция звена имеют соответственно следующий вид:
, (1.28)
, (1.29)
где 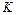– коэффициент усиления.
Передаточная функция реального интегрирующего звена записывается, как
, (1.30)
где – коэффициент усиления;
– постоянная времени.
Уравнение и передаточная функция инерционного звена 1-го порядка имеют соответственно следующий вид:
, (1.31)
, (1.32)
где 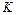– коэффициент усиления;
– постоянная времени, имеющая размерность времени.
Изменение знака любого из элементов уравнения (1.31) приведет к существенному изменению его характеристик. Звено, описываемое уравнением вида
, (1.33)
носит название неустойчивого инерционного звена 1-го порядка и имеет передаточную функцию
.
Уравнение и передаточная функция колебательного звена 2-го порядка имеют соответственно следующий вид:
, (1.34)
, (1.35)
где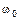 
– собственная частота колебаний;
– коэффициент затухания, принимающий значения 
.
Частным случаем колебательного звена 2-го порядка является консервативное звено, для которого коэффициент затухания 
и, следовательно, передаточная функция принимает вид
. (1.36)
Звенья, содержащие в уравнении производные по времени от входного сигнала, носят название форсирующих звеньев или звеньев с воздействием по производной.
Звено с воздействием по 1-й производной описывается уравнением
(1.37)
и имеет передаточную функцию вида
. (1.38)
