В 1932 г. американский ученый Г. Найквист вывел критерий, который дает необходимые и достаточные условия устойчивости систем с обратной связью. Этот критерий позволяет судить об устойчивости замкнутой системы по характеристике (годографу) разомкнутой системы.
Пусть 
– передаточная функция разомкнутой системы 
-го порядка, для которой граница устойчивости определятся точкой с координатами 
. Тогда для замкнутой системы с передаточной функцией 
точка границы устойчивости сместится по оси абсцисс влево на единицу, и ее координатами будут 
.
Для систем, устойчивых в разомкнутом состоянии, критерий Найквиста формулируется следующим образом: для того чтобы устойчивая разомкнутая система оставалась устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы годограф комплексной частотной характеристики разомкнутой системы не охватывал точку с координатами при изменении частоты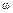 
в пределах 
.
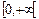Термин «не охватывает точку» означает, что приращение угла поворота вектора, проведенного из точки с координатами к годографу, при изменении частоты в указанных пределах принимает нулевое значение 
. В противном случае, если 
, считают, что годограф точку охватывает.
Годограф Найквиста для различных типов разомкнутых систем представлен на рисунке 2.1.
а) замкнутая система устойчива б) замкнутая система неустойчива
Рисунок 2.1 – Годограф Найквиста устойчивой разомкнутой системы
В соответствии с критерием Найквиста об устойчивости замкнутой системы можно судить не только по годографу, но и совместно по АЧХ и ФЧХ разомкнутой системы. Устойчивость будет иметь место, если при граничной частоте, на которой абсолютное значение фазы разомкнутой системы равно 
, амплитудная частотная характеристика будет меньше единицы: при 
.
Из критерия Найквиста следует, что нахождение замкнутой системы на границе устойчивости соответствует прохождению годографа разомкнутой системы через точку с координатами 
.
