К временным характеристикам систем автоматического управления относятся переходная функция и импульсная характеристика.
Переходной функцией системы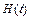 
называют ее отклик на входное воздействие в виде единичной ступенчатой функции при условии, что на момент поступления воздействия система находилась в покое (что соответствует нулевым начальным условиям).
Единичная ступенчатая функция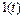 
(функция Хевисайда, или функция включения) представляет собой воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным (рисунок 1.10).
Рисунок 1.10 – Единичная ступенчатая функция
Функция включения может быть описана равенством
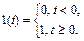
Таким образом, для переходной функции справедливо следующее соотношение:
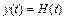при 
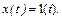
Выражение, связывающее изображение переходной функции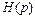 
и передаточную функцию системы 
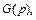имеет вид:
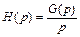. (1.17)
Используя выражение (1.17) и осуществив переход к оригиналу, можно определить переходную функцию системы с заданной передаточной функцией.
Импульсной характеристикой системы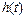 
называют ее отклик на входное воздействие в виде дельта-функции при условии, что на момент поступления воздействия система находилась в покое.
Дельта-функция – это математическая идеализация предельно короткого импульсного сигнала. Иными словами, это импульс бесконечно большой амплитуды и бесконечно малой длительности, площадь которого равна единице. Дельта-функция определяется следующими соотношениями:
.
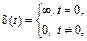
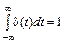Дельта-функция просто связана с единичной ступенчатой функцией:
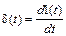. (1.18)
На графике дельта-функцию условно изображают в виде утолщения на оси ординат (рисунок 1.11).
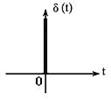
Рисунок 1.11 – Дельта-функция
Для импульсной характеристики справедливо следующее соотношение:
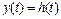при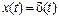 
.
Выражение, связывающее изображение импульсной характеристики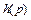 
и передаточную функцию системы 
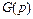, имеет вид:
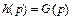. (1.19)
Согласно формуле (1.18) переходная и импульсная функции связаны соотношением
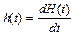. (1.20)
Пример 9. Найти переходную функцию системы, передаточная функция которой имеет вид
.
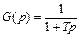Согласно выражению (1.17) изображение искомой функции определяется выражением
.
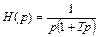Выполнив обратное преобразование Лапласа (например, с помощью таблицы 1), получим выражение для переходной функции системы:
.
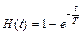Пример 10. Найти импульсную характеристику системы, передаточная функция которой имеет вид
.
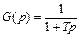Согласно выражению (1.19) изображение искомой функции определяется выражением
.
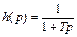Выполнив обратное преобразование Лапласа, получим выражение для импульсной характеристики системы:
.
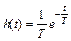Решение возможно и при использовании выражения (1.20) и результата примера 9:
.
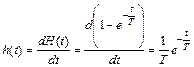