Частотная характеристика описывает установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на его входе.
Частотная характеристика звена может быть легко получена по виду передаточной функции, полагая в ней аргумент 
:
. (1.12)
Частотную характеристику можно представить в показательном виде:
, (1.13)
где 
– амплитудная частотная характеристика (АЧХ);
– фазовая частотная характеристика (ФЧХ).
Амплитудная частотная характеристика звена на частоте входного сигнала представляет собой отношение амплитуды установившегося выходного гармонического сигнала к амплитуде входного гармонического сигнала.
Фазовая частотная характеристика звена на частоте входного сигнала показывает, на сколько выходной сигнал сдвинут по фазе (углу) относительно входного сигнала.
Для частотной характеристики используется также и алгебраическая форма записи:
, (1.14)
где 
– действительная и мнимая части соответственно.
Согласно выражениям (1.13), (1.14) справедлива следующая связь между приведенными характеристиками:
, (1.15)
. (1.16)
Учитывая правила преобразования передаточных функций и выражение (1.13), можно утверждать, что при последовательном соединении звеньев их амплитудные частотные характеристики перемножаются, а фазовые частотные характеристики складываются.
Годографом частотной характеристики называют траекторию, которую описывает конец радиус-вектора, длина которого равна АЧХ системы, а угол поворота – ФЧХ. Координатами годографа в комплексной плоскости являются функции 
при изменении аргумента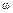 
в пределах 
.
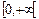Пример 8. Вывести выражения для амплитудной и фазовой частотных характеристик звена с передаточной функцией вида
.
Частотная характеристика звена запишется, как
.
Для определения АЧХ и ФЧХ звена выделим в частотной характеристике согласно выражению (1.14) действительную и мнимую части. Для этого домножим числитель и знаменатель частотной характеристики на величину, комплексно сопряженную выражению в знаменателе:
.
В итоге действительная часть частотной характеристики примет вид
,
а мнимая часть – 
.
Используя правила (1.15), (1.16), определим АЧХ и ФЧХ звена:
Те же результаты можно получить, используя иные правила расчета АЧХ и ФЧХ звена по виду частотной характеристики.
Амплитудная составляющая может быть найдена как отношение модулей выражений в числителе и знаменателе частотной характеристики, а фазовая составляющая – как разность фазовых углов функций числителя и знаменателя частотной характеристики.
Для рассматривавемого примера получим:
