Различные по физической природе объекты управления могут описываться однотипными математическими зависимостями. Эта особенность положена в основу метода математических аналогий, широко используемого в теории автоматического управления.
Построение любой системы управления начинается с изучения объекта управления и составления его математического описания, которое может быть получено экспериментальным, аналитическим или комбинированным путем.
В первом случае уравнения объекта получают путем постановки специальных экспериментов на объекте (метод активного эксперимента) либо статистической обработкой результатов длительной регистрации координат объекта в условиях его нормальной эксплуатации (метод пассивного эксперимента).
При аналитическом описании уравнения объекта получают на основании физико-химических закономерностей протекающих в нем процессов.
Комбинированный путь получения математического описания объектов подразумевает обычно составление уравнений аналитическим путем с последующим уточнением коэффициентов этих уравнений экспериментальным методом.
Уравнения объектов автоматического регулирования в зависимости от описываемого ими режима работы подразделяются на уравнения статики и динамики.
Уравнения статики описывают установившийся режим, при котором все координаты объекта остаются неизменными во времени, то есть объект находится в состоянии равновесия. Они представляют собой алгебраические или дифференциальные уравнения, содержащие производные по какому-либо параметру, кроме времени. Существенной особенностью уравнений статики является неизменность координат объекта во времени.
Уравнения динамики описывают неустановившийся или переходный режим в объекте. Выходная координата объекта при этом является функцией времени, и в общем виде уравнение динамики будет дифференциальным уравнением, содержащим производные по времени.
Вид уравнений статики и динамики определяется характером самого объекта управления и числом независимых координат, однозначно определяющих состояние объекта в каждый момент времени – числом степеней свободы.
В зависимости от числа степеней свободы все объекты можно разделить на два класса:
1) объекты с сосредоточенными параметрами, которые обладают конечным числом степеней свободы и описываются обыкновенными дифференциальными уравнениями;
2) объекты с распределенными параметрами, которые имеют бесконечное число степеней свободы и описываются дифференциальными уравнениями в частных производных.
Коэффициенты этих дифференциальных уравнений характеризуют конструктивные особенности объекта, физические и химические свойства веществ, а также различные гидродинамические и тепловые константы. Обычно все эти показатели называют «параметрами»
объекта.
Объекты, параметры которых неизменны во времени, называются стационарными и описываются уравнениями с постоянными коэффициентами. Свойства нестационарных объектов изменяются с течением времени, что отражается на соответствующих уравнениях, коэффициенты которых также становятся функциями времени.
Большинство технологических объектов регулирования является нестационарными объектами, однако скорость изменения их свойств намного меньше скорости процессов регулирования. Такие объекты можно приближенно рассматривать как стационарные в течение определенного промежутка времени.
Объекты управления называются линейными, если они подчиняются принципу суперпозиции, который заключается в том, что реакция объекта на сумму входных сигналов равна сумме реакций на каждый из сигналов в отдельности. Линейные объекты описываются линейными дифференциальными уравнениями, то есть уравнениями, в которых искомая функция и ее производные содержатся в первой степени.
Для линейного стационарного объекта с сосредоточенными параметрами уравнение состояния в общем случае может быть записано в виде:
(1.1)
где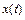 
– входной сигнал;
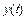– выходной сигнал;
– постоянные.
Применение линейных дифференциальных уравнений позволяет использовать мощные математические средства синтеза систем управления. Однако на практике строго линейных систем не существует, поскольку любая статическая или динамическая характеристика системы может быть линейна только на определенном участке (например, на определенном интервале частот), и, кроме того, стабильность этой характеристики может быть зависима от ряда факторов, изменяющихся во времени.
Пример 1. Составить дифференциальное уравнение для электрической системы в виде RC -схемы, в которой за входное воздействие принято напряжение 
, а за выходной сигнал – напряжение 
(рисунок 1.2).
Ток в цепи определяется током через конденсатор:
.
Рисунок 1.2 – RC -схема
По закону Кирхгофа справедливо следующее соотношение:
Обозначая 
, получим дифференциальное уравнение 1-го порядка, описывающее поведение рассматриваемой электрической системы:
. (1.2)
Пример 2. Составить дифференциальное уравнение для системы, представляющей собой гидравлическую емкость цилиндрической формы, в которую поступает жидкость с объемной скоростью 
. Площадь основания емкости – 
, высота слоя жидкости – 
(рису-нок 1.3).
Рисунок 1.3 – Гидравлическая емкость
Изменение объема жидкости в емкости определяется соотношением
,
где 
– объем жидкости.
Учитывая, что объем цилиндра определяется по правилу
,
уравнение, описывающее изменение уровня жидкости в рассматриваемой емкости, примет вид:
. (1.3)
Пример 3. Составить дифференциальное уравнение для системы, представляющей собой гидравлическую емкость цилиндрической формы, в которую поступает жидкость с объемной скоростью и вытекает через отверстие в днище площадью 
с объемной скоростью 
. Площадь основания емкости – , высота слоя жидкости – (рисунок 1.4).
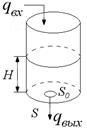
Рисунок 1.4 – Гидравлическая емкость со стоком
В данном случае изменение объема жидкости в емкости будет определяться разностью объемных скоростей подачи и истечения жидкости:
.
При равенстве притока и стока жидкости в системе будет наблюдаться стационарный режим, соответствующий постоянному уровню жидкости 
.
Учтем, что скорость истечения жидкости зависит от высоты слоя жидкости в емкости по соотношению
,
где k – коэффициент пропорциональности, зависящий от свойств жидкости, ускорения свободного падения и площади отверстия в днище.
В итоге поведение рассматриваемой системы будет описываться нелинейным дифференциальным уравнением следующего вида:
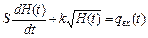. (1.4)
