Безопасность строительных конструкций гарантируется расчетом на прочность и устойчивость, который определяет необходимые соотношения между внешними воздействиями с одной стороны и геометрическими размерами элементов конструкций, а также механическими свойствами материалов – с другой. Эти соотношения представляют собой неравенства, ограничивающие область безопасной работы конструкций.
Вместе с тем расчет конструкций имеет другую цель - экономическую - максимально снизить их стоимость или наиболее выгодно использовать несущую способность конструкций, обеспечив восприятие ими максимальной нагрузки.
В детерминистической постановке эта задача не вызывает затруднений и обычно определение безопасных и наиболее выгодных соотношений между несущей способностью и стоимостью конструкций представляет собой одну и ту же двойственную задачу математического программирования.
Вопрос усложняется, если учитывать случайный характер величин, входящих в расчет, однако, в большинстве случаев это совершенно необходимо.
Например, прочность даже такого достаточно хорошо стандартизированного материала, как сталь, имеет значительный разброс с коэффициентом вариации fs ≤0. Особенно большой разброс имеют внешние воздействия, в частности нагрузки, большинство которых представляют собой случайные функции времени. Размеры поперечных сечений (даже стандартных профилей, особенно тонкостенных) имеют значительные допуски, а следовательно, и статистический разброс.
Учет случайного характера величин и функций, входящих в формулу расчета строительных конструкций и сооружений, представляет собой главную задачу теории расчета их на безопасность и максимальную экономичность.
В теории безопасности строительных конструкций все расчетные величины разделяются на две группы:
· параметры прочности, включающие в себя все характеристики, относящиеся к свойствам самой конструкции;
· параметры нагрузки, характеризующие внешние воздействия.
Разделение расчетных величин на две основные группы позволяет сформулировать задачу расчета конструкций на безопасность в виде требования о выполнении с некоторой достаточно большой вероятностью неравенства
, (III.1)
где 
– обобщенная нагрузка(наибольшее значение усилия или напряжения в конструкции, выраженное через внешнюю нагрузку);
– обобщенная прочность конструкции (несущая способность, выраженная в тех же единицах, что и обобщенная нагрузка и отвечающая предельному состоянию конструкции по прочности – предел текучести, предел прочности, пластический момент и др.).
Условие неразрушимости (III.1) может быть записано в виде
(III.2)
где 
–резерв прочности.
и могут зависеть от ряда детерминированных и случайных величин. В общем случае и являются случайными функциями, но в рассматриваемой постановке это случайные величины с заданными законами распределения. Статистические характеристики величин и (mR, 
R и mF, F) находятся самостоятельно, независимо друг от друга.
Неравенство (III.1) определяет область допустимых состояний, а уравнение
(III.3)
границу области допустимых состояний.
Вероятность выполнения неравенства
P (
) или P (S> 0) (III.4)
называется вероятностью неразрушимости конструкции, а вероятность
V=P (S<0)=1– P (S> 0) (III.5)
есть вероятность отказа.
Очевидно, что (рис. 10, а)
Ps (0), (III.6)
где p (S) – плотность вероятности резерва прочности,
Ps (S) – функция распределения резерва прочности.
При любых законах распределения 
и 
выполняются зависимости
, (III.7)
DS=DR+DF, или 
, (III.8)
где 
– математическое ожидание соответствующих случайных величин;
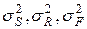– дисперсии
Число стандартов, укладывающихся в интервале [0, 
] называется характеристикой безопасности 
:
. (III.9)
Как следует из (III.9), значение характеристики безопасности bможно оценить с достаточной для практики точностью на основании только числовых характеристик случайных величин и – их математических ожиданий и дисперсий. Кроме того, при изменении значения нагрузки, например, в результате увеличения площади, с которой она собирается, равно как при изменении прочности несущих элементов, например, вследствие увеличения размеров поперечных сечений, значения изменчивости (коэффициентов вариации fR и fF остаются постоянными.
Рис. 10. Плотность распределения а) и функция распределения б) случайной величины резерва прочности S
Соотношение между вероятностью разрушения V и характеристикой безопасности может быть проиллюстрировано, если предположить, что величины и подчиняются нормальному закону распределения. Тогда и случайная величина резерва прочности также будет подчиняться нормальному закону (рис. 10). В этом случае вероятность отказа можно выразить в виде
(III.10)
Выполнив замену переменной 
, получим
, (III.11)
где Ф (u) – интеграл вероятностей. Функция (III.11) является функцией распределения для нормально распределенной случайной величины с параметрами m= 0 и s = 1.
Используя (III.9) и (III.11), получим
V = 
; P(S>0)= 1 –V = 
(III.12)
Кроме интеграла (III.11) для расчетов используется интеграл вероятностей
(III.11’)
В этом случае вероятность отказа V и вероятность безотказной работы вычисляется по формулам
V = P (S> 0)=1– V = 
(III.12’)
В таблице 5 приведены значения вероятности разрушения V для некоторых величин характеристики безопасности . Значения >5 считаются очень большими, соответствующими крайне малой вероятности разрушения.
Таблица 5
| b | 2,25 | 3,25 | 3,75 | 4,25 | 4,75 | 5,25 |
| V | 10-2 | 10-3 | 10-4 | 10-5 | 10-6 | 10-7 |
По сравнению с вероятностью разрушения V характеристика безопасности b имеет то преимущество, что выражена небольшим числом, обычно больше единицы, в то время как V представляет собой очень малую дробь. Поэтому в практических расчетах удобнее пользоваться именно характеристикой безопасности.
Как следует из таблицы 5, увеличение характеристики безопасности соответствует уменьшению вероятности отказа, или повышению вероятности безотказной работы конструкции.
Иногда вместо резерва прочности используется величина, которая может рассматриваться как интегральный коэффициент запаса
(III.13)
Коэффициент запаса связан с характеристикой безопасности и статистическими характеристиками обобщенной прочности и обобщенной нагрузки (MR, 
R и MF, F) зависимостью
, (III.14)
где 
– коэффициенты вариации.
При проектировании строительных конструкций уровень безопасности их должен быть таким, чтобы исключить возникновение отказов, связанных с угрозой для здоровья и жизни людей, опасностью для окружающей среды, а также серьезным экономическим и моральным ущербом, либо уменьшить риск наступления таких ситуаций до значений, сопоставимых с приемлемыми значениями индивидуального естественного риска.
Для строительных систем приемлемым уровнем риска считается риск при b=3, что соответствует правилу трех стандартов для допустимых отклонений случайной величины от центра распределения (математического ожидания mS). Вероятность разрушения при этом для нормального распределения равна V =0,00137.
