На практике часто встречаются случаи, когда исследуемая функция случайных величин не является строго линейной, но мало отличается от таковой и при решении задачи может приближенно рассматриваться как линейная. Такое допущение возможно в том случае, когда случайные изменения параметров 
незначительны (5 … 25%). Величина статистической изменчивости случайных параметров строительных конструкций соответствует этим требованиям.
Для вычисления статистических характеристик таких функций проводится их линеаризация путем разложения в ряд Тейлора в окрестности центра распределения случайных аргументов (в точке математического ожидания случайной функции).
Пусть имеется n случайных величин () с заданными числовыми характеристиками: математическими ожиданиями mxi, дисперсиями Dxi и корреляционными моментами Kxixj (i= 1,... n). Работа системы описывается функцией мало отличающейся от линейной:
. (II.3)
Требуется найти числовые характеристики случайной величины 
: my; Dy.
Ряд Тейлора около точки (mx1,mx2,...,mxn) с сохранением только членов первого порядка имеет вид:
(II.4)
Применив к этой функции способы определения числовых характеристик линейных функций, получим следующие зависимости:
, (II.5)
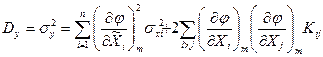, (II.6)
где 
.
При Kij= 0 (i¹j)
(II.6’)
Эти формулы находят широкое применение в прикладных задачах.
