Метод статистического моделирования на ЭВМ – это мощный универсальный метод расчета широкого класса вероятностных задач. Особенно он эффективен для нелинейных систем, аналитическое решение которых удается получить только в частных случаях.
Пусть
, (2.8)
где 
– входные случайные параметры системы (нагрузка, прочность материалов и др.);
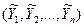– реакция системы (перемещения, напряжения, усилия и др.);
Н – оператор системы, представляющий собой уравнение, систему уравнений (алгебраических дифференциальных и др.), либо другие соотношения, с помощью которых описывается работа системы.
Для определения статистических характеристик реакции системы необходимо знать статистические характеристики входных параметров: mXi, DXi, KXiXj. Кроме того, оператор H должен быть представлен в виде моделирующего алгоритма.
Общая схема реализации метода статистических испытаний на ЭВМ представлена на рис. 9.
Рис. 9. Схема метода статистических испытаний
На схеме представлены три основных блока.
Первый блок – это генератор входных воздействий. Любой современный язык программирования содержит специальную стандартную функцию – датчик случайных чисел с равномерным распределением, генерирующую при каждом обращении к ней квазислучайное число. На основе этой программы строятся датчики случайных чисел с любым законом распределения, моделирующие случайные величины, а также случайные вектора (системы случайных величин) и случайные функции (случайные величины, изменяющиеся во времени или по координате) по их заданным вероятностным характеристикам.
Блок «Генератор входных воздействий» содержит комплекс программ моделирования реализаций входных случайных параметров.
Второй блок представляет собой детерминированную модель системы (уравнения, описывающие ее работу). Модель системы должна быть выбрана таким образом, чтобы скорость реализации базового детерминированного алгоритма на ЭВМ была достаточно высока.
Третий блок – вычисление статистических оценок реакции системы - математических ожиданий, дисперсий, законов распределения, корреляционных и спектральных характеристик обычными методами теории вероятностей.
