В практических приложениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной случайной величиной, а двумя или более случайных величин, образующими систему. Систему случайных величин можно описать в виде многомерных законов распределения  , либо приближенно при помощи статистических характеристик.
, либо приближенно при помощи статистических характеристик.
При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией. Например, систему из двух случайных величин  можно изобразить случайной точкой на плоскости с координатами
можно изобразить случайной точкой на плоскости с координатами 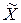 и
и  (рис. 8, а).
(рис. 8, а).


Рис. 8. Система двух случайных величин:
а) – графическая интерпретация; б) – положительная корреляция величин  и
и  ; в) – отрицательная корреляция величин
; в) – отрицательная корреляция величин  и
и  ; г) – величины
; г) – величины  и
и  некоррелированы.
некоррелированы.
Совокупность математических ожиданий mx, my представляет собой характеристику положения системы. Геометрически – это координаты средней точки на плоскости, вокруг которой происходит рассеивание.
Рассеивание случайной точки в направлении осей OX и OY характеризует дисперсии величин 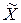 и
и  : Dx и Dy .
: Dx и Dy .
При изучении систем случайных величин всегда следует обращать внимание на степень и характер их зависимости. Понятие о зависимости случайных величин – одно из важнейших понятий теории вероятностей, где мы встречаемся с более общим типом зависимости, чем функциональная – вероятностной или статистической зависимостью.
Если случайные величины 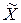 и
и  находятся в вероятностной зависимости, то это не означает, что с изменением величины
находятся в вероятностной зависимости, то это не означает, что с изменением величины 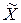 величина
величина  изменяется вполне определенным образом (как при функциональной зависимости двух величин); это лишь означает, что с изменением величины
изменяется вполне определенным образом (как при функциональной зависимости двух величин); это лишь означает, что с изменением величины 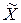 величина
величина  имеет тенденцию также изменяться (например, возрастать или убывать при возрастании
имеет тенденцию также изменяться (например, возрастать или убывать при возрастании 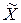 ). Эта тенденция соблюдается лишь в среднем, и в каждом отдельном случае от нее возможны отступления.
). Эта тенденция соблюдается лишь в среднем, и в каждом отдельном случае от нее возможны отступления.
Численно статистическая зависимость между двумя случайными величинами выражается при помощи корреляционного момента, который вычисляется по формулам:
· для дискретной случайной величины
 , (II.1)
, (II.1)
или
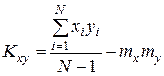 . (II.1)
. (II.1)
· для непрерывной случайной величины
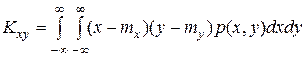 (II.1)
(II.1)
В случае, если X=Y, корреляционный момент равен дисперсии случайной величины 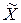 : Kxy=Dx.
: Kxy=Dx.
В практических задачах для оценки степени корреляции между двумя величинами удобнее пользоваться относительной характеристикой, называемой коэффициентом корреляции:
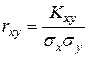 , (II.2)
, (II.2)
где  .
.
Если rxy>0, то между случайными величинами 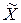 и
и  существует положительная корреляционная зависимость. Это означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать (рис. 8, б).
существует положительная корреляционная зависимость. Это означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать (рис. 8, б).
При отрицательной корреляции rxy >0, что означает, что при возрастании одной случайной величины другая имеет тенденцию убывать (рис. 8, в)
При rxy =0 случайные величины статистически независимы (рис. 8, г).
Если  , то можно считать, что рассматриваемые величины
, то можно считать, что рассматриваемые величины 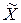 и
и  связаны функциональной зависимостью.
связаны функциональной зависимостью.






