В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того известно, что в пределах этого интервала все значения случайной величины одинаково вероятны. О таких случайных величинах говорят, что они распределены по закону равномерной плотности.
На рис. 3, а показано вертикально поставленное симметричное колесо, которое приводится во вращение и затем останавливается вследствие трения. Рассматривается случайная величина 
– угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса OА. Очевидно, величина распределена с равномерной плотностью на участке (0;2 
).
Плотность вероятностей равномерно распределенной случайной величины X на участке 
вычисляется по формуле (рис. 3, б)
. (I.10)
Так как площадь под кривой распределения всегда равно единице, то
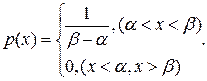(I.11)
Функция распределения F(x) вычисляется как площадь кривой распределения, лежащей левее точки x. Следовательно,
. (I.12)
График функции F(x) приведен на рис. 3, в.
Математическое ожидание величины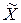 
равно:
. (I.13)
Дисперсия 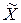равна
, (I.14)
откуда среднее квадратическое отклонение
. (I.15)
Рис. 3. Закон равномерной плотности:
а) – случайная величина q; б) – плотность распределения p (x); в) – функция распределения F (x)
