Нормальный закон распределения

Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. Сумму достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения приближенно можно описать нормальным законом, и это выполняется тем точнее, чем большее количество случайных величин суммируется.

Это распределение наиболее часто используется для описания распределений прочности строительных материалов и конструкций.

Нормальный закон распределения случайной величины 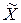характеризуется плотностью вероятности вида:

(I.16)

Кривая распределения нормального закона имеет симметричный вид. Максимальная ордината кривой, равная , соответствует точке математического ожидания x=m; по мере удаления от точки m плотность распределения падает, и при кривая асимптотически приближается к оси абсцисс. Если изменять центр рассеивания m, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 4, а).

Рис. 4. Графики плотности вероятностей нормального закона распределения:

а) при D_x = D_{x 1}= D_{x 2}= D_{x 3}=const; б) при m_x = m_{x 1}= m_{x 2}= m_{x 3}=const

Параметр – среднее квадратическое отклонение случайной величины 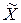– характеризует не положение, а саму форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна – при увеличении максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении – кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс, напротив, при уменьшении – кривая распределения вытягивается вверх, одновременно сжимаясь с боков (рис. 4, б).

Функция распределения случайной величины 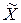, распределенной по нормальному закону с параметрами m и имеет вид:

. (I.17)

Сделаем в интеграле (I.17) замену переменной и приведем его к виду:

. (I.18)

Интеграл (I.18) называется интегралом вероятностей, его значения находятся по таблицам (см. приложение). Интеграл вероятностей обозначается как Ф^*(x), он представляет собой функцию распределения нормально распределенной случайной величины с параметрами m= 0 и =1.

Функцию распределения (I.17) случайной величины 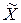с параметрами m и можно выразить через нормальную функцию распределения Ф^*(x):

. (I.19)