g cos 9

Е —1

 

§ 11. Полная свободная энергия диэлектрического тела

Полная свободная энергия ¥ (или полная внутренняя энер­гия 41), как она была определена в предыдущем параграфе, включает в себя также и энергию внешнего электрического поля, поляризующего диэлектрик; это поле можно представлять себе как создаваемое определенной совокупностью проводников с за­данными полными зарядами на них. Наряду с этой величиной ¥ имеет смысл рассмотреть полную свободную энергию, из ко­торой исключена энергия поля, которое существовало бы во всем пространстве в отсутствие тела. Обозначим напряженность по­следнего посредством (В. Тогда «полная» в указанном смысле свободная энергия равна интегралу

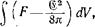
(ИЛ)

где F— плотность свободной энергии. Мы будем здесь обозначать эту величину той же буквой ¥, которой в § 10 обозначался

интеграл ] F dV. Следует подчеркнуть, что разница между обоими определениями ¥ сводится к величине, не зависящей от термо­динамического состояния и свойств диэлектрика, и потому вообще не отражается на основных термодинамических дифференциаль­ных соотношениях, которые имеют место для этой величины¹).

Вычислим изменение ¥ в результате бесконечно малого из­менения поля, происходящего при постоянной температуре и без нарушения термодинамического равновесия среды.

^J) Отметим, что вычитать из F величину £²/8л не имело бы смысла, так как Е есть поле, уже измененное присутствием диэлектрика, и потому раз­ность F — (£²/8я) отнюдь нельзя было бы рассматривать как плотность сво­бодной энергии диэлектрика как такового.

Поскольку 6/⁼' = -^-E6D, то имеем

б,Г = A- J (Е 6D — в б®) dV.

Это выражение можно тождественно переписать в виде

⁶¹=iI<^D-^6->^бс?^+iI^Е<^6D-^6с')^dv-iI(°-^Е)^шdv-

(11,2)

В первом интеграле пишем 6с* =— §гас!бф₀ (ф₀ — потенциал поля Щ и преобразуем его по частям:

J grad б_Фо (D—Щ dV = J б_Фо (d—<g) df — J б_Фо div (d—в) dV.

Легко видеть, что оба интеграла в правой части равенства обра­щаются в нуль. Для объемного интеграла это следует непосред­ственно из уравнений divD = 0 и div© = 0, которым удовлетво­ряют соответственно поле в диэлектрике и поле в пустоте. Первый же интеграл берется по поверхности создающих поле проводни­ков и по бесконечно удаленной поверхности. Последний интеграл обращается, как обычно, в нуль, а на каждом из проводников бф₀ = const, так что

<£б_Фо (D — ®)df = бф₀^ (D—G) df.

Но поле (€•, по определению, создается теми же источниками, что и поле Е с индукцией D (т. е. одними и теми же провод­никами с заданными полными зарядами е на них). Поэтому оба

интеграла &D_ndf и (f)($:_ndf равны одной и той же величине 4яе, а их разность равна нулю.

Аналогичным образом убеждаемся в том, что равен нулю и второй член в (11,2) (для этого подставляем в нем Е =■= — grad ф и производим такое же преобразование). Окончательно получается

бг ==_ j_J(d—E)6edK=—jp6edv. (П,3)

Замечательно, что в этом выражении интеграл берется только по объему, занятому диэлектрической средой, так как вне тела Р = 0.

Подчеркнем, однако, что подынтегральное выражение Р6© не может быть истолковано как вариация «плотности» свободной энергии тела, подобно тому, как это было сделано в связи с фор­мулами (10,3), (10,4). Прежде всего, эта «плотность» должна су­ществовать и вне тела, так как его наличие искажает поле и в окружающем пространстве. Ясно также, что плотность энер­гии в каждой точке тела может зависеть лишь от реально су-

шествующего в ней поля, а не от поля, которое имелось бы здесь в отсутствие тела.

Если внешнее поле @ однородно, то

6<F = -6e-$Pdi/= — ^»бе, (11,4)

где —полный электрический дипольный момент тела. Поэтому термодинамическое тождество для свободной энергии можно на­писать в данном случае как

d¥ = — <ydT — _<p>d®. (11,5)

Полный электрический момент тела можно, следовательно, полу­чить путем дифференцирования полной свободной энергии:

 

 

Отметим, что последнюю формулу можно получить и непо­средственно из общей статистической формулы

 

дХ \ дк ] т '

где Ж—-гамильтониан тела как системы составляющих его час­тиц, а "к — какой-либо параметр, характеризующий внешние усло­вия, в которых находится тело (см. V (11,4), (15,11)). Для тела, находящегося во внешнем однородном поле О?, гамильтониан содержит член —где — оператор дипольного момента, и, выбрав 05 в качестве параметра К, мы получим искомую фор­мулу.

Если D и Е связаны друг с другом линейной зависимостью D = eE, то аналогичным путем можно вычислить в явном виде не только вариацию 6<F, но и саму <F. Имеем

 

 

Это выражение тождественно переписываем в виде.

=i1<^Е+^е)<^D-®)^dy—кI ®(°~^Е)м.

Первый член в правой части равенства обращается в нуль, в чем можно убедиться, положив в нем E-f-0? =— grad (ср + ф₀) и про­изведя преобразование, вполне аналогичное произведенному выше. Поэтому получаем

F-f₀(V, T) = -\^WdV. (11,7)

В частности, в однородном внешнем поле

f-f₀(l/, Т) = -Ч&&. (11,8)

Последнее равенство можно было бы получить и путем не­посредственного интегрирования соотношения (11,3), если заме­тить, что в силу линейности всех уравнений поля (при D = eE) электрический момент должен быть линейной функцией ©.

Линейную зависимость между компонентами и можно написать в виде

*/ = V«,*®*, (11,9)

подобно тому, как это было сделано нами для проводников (§ 2). В отличие от проводников, однако, «поляризуемость» диэлектри­ческого тела зависит не только от его формы, но и от его ди­электрической постоянной. Симметричность тензора <x_ik (упомя­нутая уже в § 2) непосредственно следует из соотношения (11,6); достаточно заметить, что вторая производная

д²<Г ЗУ/

 

не зависит от порядка дифференцирования.

Формула (11,7) еще более упрощается в важном случае, когда е близко к 1, т. е. диэлектрическая восприимчивость х = (е—1)/4л мала. В этом случае при вычислении энергии можно пренебречь вызываемым наличием тела искажением поля, т. е. положить

Р = хЕ л? х©.

Тогда

IF— <F₀= —- у J(S²dV, (11,10)

где интеграл берется по объему тела. В однородном поле диполь-ный момент _t^^, = Vx6-, а свободная энергия

f-f₀ = -^g². (11,11)

В общем случае произвольной зависимости D от Е простые формулы (11,7) и (11,8) не имеют места. Для вычисления W здесь может быть полезной формула

8л 2

^=K^F-i£)^dv==S[^F-^-^im

dV, (11,12)

вывод которой после произведенных выше вычислении очевиден. Действительно, подынтегральные выражения в обоих интегралах отличаются на величину

ed е² 1 _/г.,„ >.

—ST-------- Г+8л-=-&т-(°-^е)(^Е+^'

после подстановки Е = — V<P, © =— V<P₀ ^и интегрирования по всему пространству это выражение обращается в нуль. Обратим внимание на то, что в (11,12) (как и в (11,7)) подынтегральное выражение (во втором интеграле) обращается в нуль вне тела (где Р = 0, F = £²/8л), так что интегрирование производится только по его объему.

 

Задача

Получить формулу, заменяющую (11,7), для тела, находящегося не в пустоте, а в среде с диэлектрической проницаемостью в^(<?>.

Решение. Повторяя для этого случая произведенные в тексте преобра­зования, получим

¥ ~¥о = - J6-(D-e«)E) dV.

 

§12. Электрострикция изотропных диэлектриков

Для твердого диэлектрика в электрическом поле нельзя ввести понятие давления так, как это делается для изотропного тела в отсутствие поля, потому что действующие в таком диэлектрике силы (они будут определены в §§ 15, 16) меняются вдоль тела и анизотропны, даже если тело само по себе изотропно. Точное определение деформации (электрострикции) такого тела требует решения сложной задачи теории упругости.

Дело обстоит, однако, гораздо проще, если нас интересует только изменение полного объема тела. Как уже было указано в § 5, при этом можно считать форму тела неизменной, т. е. рас­сматривать деформацию как равномерное всестороннее сжатие или растяжение.

Будем пренебрегать диэлектрическими свойствами внешней среды (например, атмосферы), в которой находится рассматри­ваемое тело, т. е. будем считать, что ее е=1. Роль среды сво­дится только к созданию равномерного давления, действующего на поверхность тела. Именно это внешнее давление мы будем обозначать ниже посредством Р. Если ¥ — полная свободная энергия тела, то согласно известному термодинамическому соот­ношению

 

 

и соответственно в выражении для дифференциала d¥ должен быть добавлен член —PdV- Так, в однородном внешнем поле имеем вместо (11,5)

d¥ = — dT - Р dV - & №.

Введем полный термодинамический потенциал тела согласно обычному термодинамическому определению:

Ф = ¥ + PV.

(12,1)

Для дифференциала этой величины (в однородном внешнем поле) имеем соотношение

с1ф = — ^ dT + VdP-tfbdV. (12,2)

Изменение термодинамических величин во внешнем электри­ческом поле является обычно относительно малой величиной. Согласно теореме о малых добавках (см. V (15,12)), малое из­менение свободной энергии (при заданных Т и V) и малое изме­нение термодинамического потенциала (при заданных Т и Р) равны друг другу. Поэтому наряду с (11,8) можно написать аналогичное соотношение

Ф = Ф₀-¹/&&> (12,3)

для термодинамического потенциала тела во внешнем однородном поле. Здесь gb„ относится к телу в отсутствие поля при задан­ных значениях Р, Т (в то время как 3~₀ в (11,8) есть свободная энергия тела в отсутствие поля при заданных значениях V и Т).

Выразив в явном виде зависимость дипольного момента от V и & согласно (11,9), перепишем (12,3) в виде

Ф = Ф₉(Р, Т)-ЧУ*_1к%%, (12,4)

причем поправочный член должен быть выражен в функции от температуры и давления согласно уравнению состояния тела в от­сутствие поля. Эта формула особенно упрощается в случае малой диэлектрической, восприимчивости вещества:

ф = ф₀(Р, Т)-^-& (12,5)

(ср. (11,11)).

Искомое изменение объема V — V₀ во внешнем поле можно получить теперь непосредственно путем дифференцирования Ф по давлению (при постоянных Т и ©). Так, из (12,5) найдем

 

Эта величина может быть как положительной, так и отрицатель­ной (в противоположность электрострикции проводников, объем которых в поле всегда возрастает).

Аналогичным образом можно вычислить также и количество тепла Q, поглощаемое в диэлектрике при изотермическом вклю­чении внешнего электрического поля (причем внешнее давление поддерживается постоянным)^J).

-¹) Если же тело теплоизолировано, то наложение поля приведет к изме­нению температуры, равному ДГ = —Q:1$p, где %р—теплоемкость тела при постоянном давлении,

Дифференцирование Ф — Ф₀ по температуре даст изменение энтропии тела, а умножив его на Т, получим искомое количество тепла. Так, из (12,5) получается

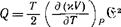
(12,7)

Положительные значения Q соответствуют поглощению тепла.

 

3 а д а ч и

1. Определить изменение объема и электрокалорический эффект для ди­электрического эллипсоида в однородном электрическом поле, параллельном одной из его осей.

Решение. Согласно формулам (12,3) и (8,10) имеем

 

8л ПЕ + 1 -

V

8л

Для изменения объема находим ^г): У-У_п (J² Г е-1

(пе+1— п) К (пе+1—п)²

 

—) 1 дР)т\ '

а для электрокалорического эффекта:

-я)2

8л

Q =

ne + 1 — п (яе+:

dV_ дТ Jp

-коэффициент сжимаемости тела, а ос =

где т= —

V I дР)т~ коэффициент теплового расширения.

В частности, для плоскопараллельной пластинки в перпендикулярном к ней поле п — \, так что

-1

гК

iZp_₌JL²

ТУФ? 8л.

8л

а(е —1). 1

дг дР дг дТ

Для такой же пластинки (или любого цилиндрического тела) в продольном поле п = 0 и

 

' 8л

Q =

Г№²

8л

i а(е —1)­

дТ

■]■

1) Положив е—>-оо, получим для изменения объема проводящего эплип- соида (V — V0)/V = Й2/8лЛ>. Для шара п = 1/3 и мы возвращаемся к резуль. тату задачи 4 § 5. 2) является теплоемкостью пластинки, помещенной между обкладками плоского конденсатора, включенного в цепь с постоянной э. д. с. В разомкну- том же конденсаторе с постоянными зарядами на обкладках пластинка будет иметь теплоемкость

2. Определить разность теплоемкости??<p плоскопараллельной пластинки в перпендикулярном к ней поле при постоянной разности потенциалов между ее сторонами и теплоемкости при постоянной индукции; в обоих случаях внешнее давление поддерживается постоянным²).

Решение. Согласно результатам задачи 1 энтропия пластинки

 

 

Индукция поля внутри пластинки совпадает с внешним полем: D = G. Поэтому для вычисления теплоемкости надо дифференцировать <ff при постоян­ном <$,. Разность потенциалов между сторонами пластинки ф = £/=(у//е, где /—толщина пластинки. При равномерном сжатии или расширении тела / ме­няется пропорционально V¹^³. Поэтому для вычисления теплоемкости ^_ф надо

дифференцировать _Qf при постоянном произведении (JK^Ve. В результате найдем для искомой разности:

3. Определить электрокалорический эффект в однородном диэлектрике,
полный объем которого поддерживается постоянным.

Решение. Строго говоря, при наложении внешнего поля плотность тела меняется (становясь неоднородной вдоль тела), даже если его полный объем поддерживается постоянным. Однако при вычислении изменения полной энтропии этим обстоятельством можно пренебречь и считать плотность р по­стоянной в каждой точке тела ').

Согласно (10,18) полная энтропия тела

 

 

где интегрирование распространяется по объему тела. Поглощаемое коли­чество тепла

 

4. Определить разность — ^_D (см. задачу 2) при постоянном полном
объеме пластинки.

Решение. При неизменном объеме (а потому и толщине) пластинки дифференцирование при постоянной разности потенциалов эквивалентно диф­ференцированию при постоянной напряженности Е.

С помощью полученной в задаче 3 формулы для энтропии находим

_ TVE* (дг у_ TV& (дг у

 

5. Конденсатор состоит из двух проводящих поверхностей, находящихся
на расстоянии h друг от друга, малом по сравнению с размерами обкладок;
пространство между обкладками заполнено веществом с диэлектрической про-
ницаемостью е_х. В конденсатор вводится шарик радиуса n^ftc диэлектриче-
ской проницаемостью е₂. Определить изменение емкости конденсатора.

Решение. Пусть шарик вводится в конденсатор так, что разность по­тенциалов ф между его обкладками остается неизменной. Роль свободной энергии при постоянных потенциалах проводников играет Jp'. В отсутствие шарика jF = —С₍|ф²_;2, где С₀ — первоначальная емкость конденсатора. Ввиду

') Изменение плотности бр — величина второго порядка по полю (—£²), а связанное с ним изменение полной энтропии—четвертого порядка. Действи-

dS С

тельно, линейное по бр изменение полной энтропии есть J SpdV, ио ин­теграл \ bpdV = 0 в силу неизменности общей массы тела.

малых размеров шарика можно считать, что он вводится в однородное поле с напряженностью ® = ф//г, а изменение мало. Малое изменение при по­стоянных потенциалах равно малому изменению при постоянных зарядах источников поля. С помощью формулы, полученной в задаче § 11, и фор­мулы (8,2) находим

^# "~ 2 ^Lo<P 2n² 2_6l + g₂ ' откуда искомая емкость

_г__г, а³ Мег — б]) ^с-^с<Н"р 2_б1 + е₂ ■

§ 13. Диэлектрические свойства кристаллов

В анизотропной диэлектрической среде (монокристалл) линей­ная связь между индукцией и напряженностью электрического поля имеет более сложный вид, не сводящийся к простой про­порциональности.

Наиболее общий вид такой зависимости дается выражением

+(13,1)

где D„—постоянный вектор, а совокупность величин e_!k состав­ляет тензор второго ранга—тензор диэлектрической проница­емости (или, короче, диэлектрический тензор). Свободный член D₀ в соотношении (13,1) существует, однако, не во всяком кри­сталле. Большинство типов кристаллографической симметрии не допускает существования постоянного вектора (см. ниже), и тогда имеем просто,

D_t = &_tkE_k. (13,2)

Тензор z_ik симметричен:

^£ik^==eki- (13,3)

Чтобы убедиться в этом, достаточно воспользоваться термоди­намическим соотношением (10,10) и заметить, что вторая про­изводная

д*РдР;

™dE_kdE; - dE_k ~^£ik

не зависит от порядка дифференцирования.

Для самой величины F имеем (при выполнении (13,2)) вы­ражение

^Р = ^ро-^§Г*' (¹³'⁴)

Свободная энергия F равна

Как и всякий симметричный тензор второго ранга, тензор e_ik путем надлежащего выбора осей координат может быть при­веден к диагональному виду. В общем случае, следовательно, тензор E_ik определяется тремя независимыми величинами—тремя главными значениями е⁽¹⁾, е⁽²⁾, е⁽³⁾. Все эти величины всегда больше единицы, подобно тому как е > 1 у изотропного тела (см. § 14).

В зависимости от той или иной симметрии кристалла число различных главных значений тензора e_ik может оказаться и меньшим трех.

В кристаллах триклинной, моноклинной и ромбической систем все три главных значения различны; эти кристаллы называются двухосными¹). При этом в кристаллах триклинной системы на­правления главных осей тензора г_1к не связаны однозначным образом с какими-либо кристаллографическими направлениями. В кристаллах моноклинной системы заранее определенным явля­ется направление одной из главных осей—она должна совпадать с осью симметрии второго порядка или быть перпендикулярной к плоскости симметрии кристалла. В кристаллах же ромбичес­кой системы кристаллографически определены все три главные оси тензора e_ik.

Далее, в кристаллах тетрагональной, ромбоэдрической и гек­сагональной систем два из трех главных значений совпадают, так что имеются всего две независимые величины; такие кри­сталлы называют одноосными. Одна из главных осей совпадает при этом с кристаллографической осью симметрии четвертого, третьего или шестого порядка, а направление двух других глав­ных осей можно выбрать произвольным образом.

Наконец, в кристаллах кубической системы все три главных значения тензора e_ik одинаковы, а направления главных осей произвольны. Это значит, что тензор г_(к имеет вид гЬ_1к, т. е. определяется одним скаляром е. Другими словами, в отношении своих диэлектрических свойств кристаллы кубической симметрии не отличаются от изотропных тел.

Все эти довольно очевидные свойства симметрии тензора &_ik становятся особенно наглядными, если воспользоваться известным из тензорной алгебры понятием тензорного эллипсоида, длина полуосей которого пропорциональна главным значениям симмет­ричного тензора второго ранга. Симметрия эллипсоида должна соответствовать при этом симметрии кристалла. Так, в одноосном кристалле тензорный эллипсоид вырождается в эллипсоид вра­щения, полностью симметричный относительно продольной оси; подчеркнем, что для физических свойств кристалла, определя­ющихся симметричным тензором второго ранга, наличие оси симметрии уже третьего порядка эквивалентно полной изотро-

^г) Это название связано с оптическими свойствами кристаллов —см. §§ 98, 99.

пии в плоскости, перпендикулярной к этой оси. В кристаллах кубической симметрии тензорный эллипсоид вырождается в сферу.

Остановимся теперь на особенностях диэлектрических свойств кристаллов с постоянным членом D₀ в (13,1). Наличие этого члена означает, что диэлектрик спонтанно поляризован и в от­сутствие внешнего электрического поля; такие тела называют пироэлектрическими. Величина этой спонтанной поляризации, однако, фактически всегда очень мала (по сравнению с молеку­лярными полями). Это обстоятельство связано с тем, что большие значения D„ приводили бы к существованию сильных полей внутри тела, что энергетически весьма невыгодно и потому не могло бы соответствовать термодинамическому равновесию. Малость D₀ обеспечивает в то же время законность разложения D по степеням Е, первыми двумя членами которого и является выражение (13,1).

Термодинамические величины пироэлектрического тела нахо­дим, интегрируя соотношение

dF

 

откуда

^^-^-^А- (¹³'⁶)

Свободная энергия

^F = ^F + = ^F° + = ^F° + ^s^ (Di-D_oi) (D_k-D_ok).

(13,7)

Отметим, что из F выпадает имевшийся в F член, линейный по

Полную свободную энергию пироэлектрика можно вычислить по формуле (11,12), подставив в нее (13,7) и (13,1). В отсутствие внешнего поля, С* = 0, получается простой результат:

^r= l(^F»—(13.8)

Отметим, что свободная энергия пироэлектрика в отсутствие внешнего поля зависит (вместе с полем Е) не только от его объема, но и от формы.

Как уже было указано, явление пироэлектричества возможно не при всякой симметрии кристалла. Поскольку при любом пре­образовании симметрии все свойства кристалла должны оставать-

^J) Следует отметить, что в этих формулах мы в действительности пренеб­регаем пьезоэффектом (т. е. влиянием внутренних напряжений на электричес­кие свойства тела, см. § 17). Поэтому они, строго говоря, применимы лишь в случае однородных по объему тела полей, когда напряжения в теле могут отсутствовать.

ся неизменными, то ясно, что пироэлектрическим может быть лишь такой кристалл, в котором существует направление, оста­ющееся неизменным (в том числе не меняющееся на обратное) при всех преобразованиях симметрии; в этом направлении и будет лежать постоянный вектор d₀.

Этому условию удовлетворяют лишь те группы симметрии, которые складываются из одной оси и проходящих через нее плоскостей симметрии. В частности, пироэлектрическими заведомо не могут быть кристаллы, обладающие центром симметрии. Пере­числим те из 32-х кристаллических классов, в которых сущест­вует пироэлектричество:

триклинная система: с,,

моноклинная система: C_s, с»,

ромбическая система: C_2v,

тетрагональная система: с₄, C_iv,

ромбоэдрическая система: C_s, C_3v,

гексагональная система: с₆, C_6v. Среди'кубических классов пироэлектрических, разумеется, вооб­ще нет. В кристалле класса С₁ направление пироэлектрического вектора d₀ не связано с каким-либо кристаллографически выде­ленным направлением, а в кристалле класса C_s должно лежать в плоскости симметрии. Во всех же остальных из перечисленных выше классов направление d₀ совпадает с направлением оси симметрии *).

*) Говоря об условиях симметрии, мы рассматриваем кристаллическую среду как неограниченную. Для конечного кристалла точное значение его полного дипольного момента может зависеть (в ионном кристалле) от того, по каким кристаллическим плоскостям проходят его грани—содержат ли эти плоскости ионы одного знака или же они электрически нейтральны. Но в рамках макроскопической электродинамики, подразумевающей усреднение по физически бесконечно малым объемам, естественно понимать как усредненное также и положение граней относительно кристаллической решетки. В результате такого усреднения значение D0 окажется равным нулю в любом непироэлектри­ческом конечном кристалле и не зависящим от огранки — в пироэлектрическом.

Следует указать, что в обычных условиях пироэлектрические кристаллы не имеют полного электрического дипольного момен­та, хотя поляризация в них и не равна нулю. Дело в том, что внутри спонтанно поляризованного диэлектрика имеется отлич­ная от нуля напряженность поля Е. Благодаря тому, что фак­тически образец обычно обладает некоторой, хотя и малой, но все же не равной нулю проводимостью, наличие поля вызовет появление тока, который будет течь до тех пор, пока образу­ющиеся на поверхности тела свободные заряды не приведут к исчезновению поля в образце. В том же направлении действуют ионы, оседающие на поверхность образца из воздуха. На опыте пироэлектрические свойства наблюдаются при нагревании тела, когда величина его спонтанной поляризации меняется и обнару­живается это изменение.

Задачи

1. Определить поле, создаваемое в пустоте пироэлектрическим шаром.

Решение. Внутри шара имеется однородное поле, в котором напряжен­ность и индукция связаны соотношением 2Е =—D (как это следует из (8,1) при ($ = 0, т. е. в отсутствие внешнего приложенного поля). Подставляя в (13,1), получим уравнение 2£, + e,'^£fe = — D_oi. Выберем оси координат вдоль главных осей тензора ъ_1к. Тогда найдем из этого уравнения

Р ₌ Dpi. Di-Ej _ 3D_0i

' 2-fe«'>' ¹ 4я 4л(2 + е<'>) "

Поле вне шара есть поле электрического диполя с электрическим моментом <p = PV.

2. Определить поле точечного заряда в однородной анизотропной среде ^х).

Решение. Поле точечного заряда описывается уравнением div D=4ne б (г) (заряд находится в начале координат). В анизотропной среде D,' = e,-^E_fe = = — е,-£ dip/дхь; выбирая оси х, у, г вдоль главных осей тензора е,-^, получим для потенциала уравнение

дх¹- ¹ ду- ¹ дг^{2 w}

Путем введения новых переменных согласно

* = *' У~е№, у = у' yeW\ z = z' Уё& (1)

оно приводится к виду

Д ф= _гб (г),

У е<*>е<.У>е<^г>

который формально отличается от уравнения для поля в пустоте лишь заме­ной е на е' =е [e<^x)eWe<^z>]~'/². Поэтому

7»

е

_1_ У _1_

е<*> ' eW ' е<^г>

В тензорных обозначениях, не предрешающих выбор системы координат,

е

ф=

е | eik x_lx_h

где |е| — определитель тензора е,-£.

3. Определить емкость проводящего шара (радиуса а), погруженного в анизотропную диэлектрическую среду.

Решение. Путем преобразования (1) определение поля шара с зарядом е в анизотропной среде сводится к определению поля в пустоте, создаваемого зарядом е', распределенным по поверхности эллипсоида

e_ikx'ixk = е<*>*'² + еО"г/'²-f e<«z'² = а².

Воспользовавшись формулой (4,14) для потенциала поля эллипсоида, по­лучим для искомой емкости:

7.

_e(.v) / V _eW 1 V ¹ е<^г>

^г) В задачах 2 — 6 диэлектрическая анизотропная среда предполагается непнроэлектрической.

4. Определить поле в плоскопараллельной анизотропной пластинке, нахо-
дящейся во внешнем однородном поле

Решение. Из условия непрерывности касательной составляющей напря­женности следует, что

Е = @ + An,

где Е — напряженность однородного поля внутри пластинки, п —единичный вектор нормали к ее поверхности и А — постоянная. Последняя определяется из условия непрерывности нормальной компоненты индукции: nD = n(S; или

nflik^Ek = ЩЦк&к + Аг_1кщп_к = ® _{щ.

Отсюда

 

^Ё1т^п1^пт

В частности, если внешнее поле направлено по нормали к пластинке (ось г), то

Д=е(1-е„)/е„. Если поле параллельно пластинке и направлено по оси х:

А = —©е_гд:/е_гг.

5. Определить момент сил, действующих на анизотропный диэлектрический
шар, находящийся (в пустоте) во внешнем однородном поле (v.

Решение. Согласно (8,2) имеем для напряженности поля внутри шара

Е 5_ К

^A'~2+e(*>^U*

(и аналогично для Е_у, Е₂), причем оси х, у, г выбраны вдоль главных осей тензора е,^. Отсюда для компонент дипольного момента шара (радиуса а)

_т 4л _„ е<*> — 1.,_гг ^ = __азр,₌ ___азс5,.

Компонента же действующего на шар момента сил

 

 

и аналогично для К_х, К_у-

6. В неограниченной анизотропной среде имеется сферическая полость.
Выразить поле в полости через однородное поле £(^е> в среде вдали от полости.

Решение. Преобразованием (1) задачи 2 уравнение для потенциала поля в среде приводится к уравнению Лапласа для поля в пустоте. Уравнение же для потенциала поля в полости, напротив, превращается в уравнение для потенциала в среде с диэлектрическими проницаемостями 1/е<*>, 1/еО", 1/е^(г>. Кроме того, шар (радиуса а) превращается в эллипсоид с полуосями а/}/"е<*>, a/]AeW, а/Уг^К Пусть ге<*>, п^{У\ п*^г> — коэффициенты деполяризации такого эллипсоида (определяемые по формулам (4,25)). Применяя к полю этого эллип­соида формулу (8,7), получим соотношение

_1г, д<р<'> п'*> дф('">_ dcp(g) ^{( П} ' дх' ■ е<*> дх' ~~ дх' (и аналогичные—вдоль осей у' и г'). Возвращаясь к прежним координатам, имеем

 

так что для поля в полости получаем окончательно
с(«) ^е(х) с<е)

_е(Л) —_n(X) (g(X) _l)

§ 14. Положительность диэлектрической восприимчивости

Для выяснения характера зависимости термодинамических величин диэлектрика в поле от его диэлектрической проница­емости рассмотрим формальную задачу об изменении электри­ческой части полной свободной энергии тела при бесконечно малом изменении е.

Для изотропного (но не обязательно однородного) диэлектри­ка имеем согласно (10,20)

При изменении е изменяется также и индукция поля. Поэтому рассматриваемая вариация свободной энергии равна

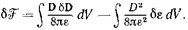Первый член в правой части равенства совпадает с выражением (10,2) для работы, совершаемой при бесконечно малом изменении источников поля (зарядов проводников). Но в данном случае мы рассматриваем изменение поля при неизменных его источниках; поэтому этот член обращается в нуль, и мы получаем

⁶^=-J^8>= 4^6e-I>-

(Н,1)

Из этой формулы следует, что всякое увеличение диэлектри­ческой проницаемости среды хотя бы в некотором ее участке (при неизменных источниках поля), приводит к уменьшению ее полной свободной энергии. В частности, можно утверждать, что свободная энергия всегда уменьшается при внесении в диэлект­рическую среду незаряженных проводников, поскольку послед­ние могут рассматриваться (в электростатике) как тела с беско­нечно большой е. Это утверждение обобщает высказанную в § 2 теорему об уменьшении энергии электростатического поля в пустоте при внесении в него незаряженного проводника.

Полная свободная энергия уменьшается и когда какой-либо заряд подносится к диэлектрическому телу из бесконечности (что можно воспринимать как увеличение е в некотором объеме поля вокруг заряда). Чтобы сделать отсюда заключение о том, что всякий заряд притягивается к диэлектрику, надо было бы, строго говоря, доказать еще, что ¥ не может достигнуть мини­мума ни при каком конечном расстоянии между зарядом и телом. Мы не станем останавливаться здесь на доказательстве этого утверждения, тем более, что появление сил притяжения между зарядом и диэлектриком можно рассматривать как довольно очевидный результат взаимодействия этого заряда с дипольным моментом поляризуемого им диэлектрика.

Непосредственно из формулы (14,1) можно сделать заключе­ние о направлении движения диэлектрического тела в квазиодно­родном поле, т. е. в поле, которое можно считать постоянным на протяжении размеров тела. В этом случае Е² выносится из-под знака интеграла и разность ¥ — ¥_в есть отрицательная величи­на, пропорциональная Е². Стремясь занять положение, в котором его свободная энергия минимальна, тело будет, следовательно, перемещаться в направлении увеличения Е.

Независимо от формулы (14,1) можно показать, что полное изменение свободной энергии диэлектрического тела при внесе­нии его в электрическое поле отрицательно¹). Это можно сделать с помощью термодинамической теории возмущений, рассматри­вая изменение свободной энергии тела как результат возмуще­ния его квантовых уровней энергии внешним электрическим полем. Согласно этой теории имеем

ЩГ__-г _j7____ 1 у у' I ^Vnm \²(W_m — W„) \__[V _y.„

n m n in

(14,2)

(см. V (32,6)). Здесь E^ — невозмущенные уровни, У_тп—матрич­ные элементы возмущающей энергии, а черта обозначает стати­стическое усреднение с помощью распределения Гиббса

 

 

Член V'_пп в формуле (14,2), линейный по полю, отличен от нуля только в пироэлектрических средах. Интересующее же нас квад­ратичное по полю изменение свободной энергии дается осталь­ными членами этой формулы; их отрицательность очевидна.

С другой стороны, из самого вывода формулы (14,2) ясно, что полная свободная энергия ¥ должна пониматься в ней в указанном в § 11 смысле—из нее исключена энергия поля, которое существовало бы в отсутствие тела. Поэтому разность ¥ — ¥₀ дается термодинамической формулой (11,7). Рассмотрим тело в виде длинного цилиндра, расположенного вдоль однород­ного внешнего поля ©. Тогда поле внутри цилиндра совпадает сб, а его поляризация Р = (е—1)($/4я, так что

*) Имеется в виду изменение, пропорциональное квадрату поля. Напомним, что в пироэлектрических телах изменение свободной энергии содержит также и линейный по полю член, который нас здесь не интересует.

 

 

Отсюда следует, что разность ¥—¥_в будет отрицательна, только если е> 1. Мы приходим к упомянутому в § 7 и использован­ному уже ранее утверждению, что диэлектрическая проницаемость

всякого тела больше единицы, т. е. его диэлектрическая вос­приимчивость х=(е—1)/4я положительна.

Таким же образом доказываются неравенства е^{П > 1 для главных значений тензора e_ik анизотропной диэлектрической среды. Для этого достаточно рассмотреть энергию поля, направ­ленного вдоль каждой из трех главных осей.

§ 15. Электрические силы в жидком диэлектрике

Вопрос о вычислении сил (их называют пондеромоторными), действующих на диэлектрик в произвольном неоднородном элек­трическом поле, довольно сложен и требует раздельного рассмот­рения для жидких (или газообразных) и твердых тел. Мы нач­нем с более простого случая жидких диэлектриков.

Будем обозначать посредством f dV силу, действующую на элемент объема среды dV, вектор f можнъ назвать объемной плотностью сил.

Как известно, силы, действующие на какой-либо конечный объем тела, могут быть сведены к силам, приложенным к по­верхности этого объема (см. VII § 2). Это обстоятельство явля­ется следствием закона сохранения импульса. Сила, действующая на вещество в объеме dV, представляет собой изменение его им­пульса в единицу времени. Это изменение должно быть равно количеству импульса, втекающего в течение того же времени в этот объем через его поверхность. Если обозначить тензор пото­ка импульса через —a_ik, то

(15,1)

где интегрирование в правой части равенства производится по поверхности объема V. Тензор a_;k называют тензором напряже­ний. Очевидно, что

Gikdf_k = e_;kn_kdf

есть 1-я компонента силы, действующей на элемент поверхности df (п—единичный вектор нормали к поверхности, внешней по отношению к данному объему).

Аналогичным образом сводится к интегралу по поверхности также и полный момент сил, действующих на данный объем, чем обеспечивается выполнение закона сохранения момента им­пульса. Как известно, возможность этого сведения связана с сим­метричностью тензора напряжений (o_ik = a_ki); последняя является, таким образом, выражением закона сохранения момента импульса.

Преобразуя интеграл по поверхности в (15,1) в интеграл по объему, получим

и отсюда, ввиду произвольности объема интегрирований,

 

 

Это — известная формула, выражающая объемные силы через тен­зор напряжений.

Приступим теперь К вычислению тензора напряжений. Каж­дый малый участок поверхности можно рассматривать как плб-ёкйй; а тело и электрическое поле вблизи него—как однородные. Поэтому для упрющения вывода мы можеМ) без всякого ограни­чения общности, рассмотреть однородный (пО составу, плотности и температуре) плоскЬпараллельньш слой вещества (толщины h), находящийся в однородном электрическом поле¹). Это поле можно представлять себе как создаваемое приложенными к поверхности слоя проводящими плоскостями (обкладками конденсатора).

Следуя общему методу определения сил, подвергнем оДну из обкладок («верхнюю») параллельному виртуальному смещению на бесконечно малую величину |; направление 1 произвольно и не обязательно Совпадает с направлением нормали п. Будем считать, что потенциал проводника (в каждой его точке) остается при смещений неизменным, а вызываемая этим смещением однородная деформация слоя диэлектрика — изотермична.

На единицу площади поверхности действует со стороны самого тела (слоя) сила —o_ikn_k. При виртуальном смещений эта сила производит работу —cr₍-_fen_fe£,-. С Другой стороны, работа₍ прбиз-водимая при изотермической деформации и постоянных потен­циалах проводников, равна убыли величины \FdV или (на еди­ницу площади поверхности слоя) величины hF. Таким образом,

e_ik$_in_k = 8(hF) = h8F + F6h. (15,3)

Термодинамические величины жидкости зависят (при данных температуре и напряженности поля) только от ее плотности; деформации, не меняющие плотности' (деформации сдвига), не отражаются на термодинамическом состоянии. Поэтому для изо­термической вариации 8F в жидкости пишем

^tf-(#)r..«+(#)..,*—^+(1)..,*-см)

*) Тем самым мы отбрасываем в тензоре напряжений члены, которые могли бы зависеть от градиентов температуры, поля и т. п. Эти члены, однако, исче-зающе малы по сравнению с членами, не содержащими производных, в том же смысле, как малы члены с производными, которые могли бы присутствовать в зависимости D от Е.

Изменение плотности слоя вещества связано с изменением его толщины соотношением бр = — p8h/h. Вариация же поля вычис­ляется следующим образом.

В данную точку пространства (с радиус-вектором г) попадает при смещении вещество из точки г — и, где и — вектор смещения частиц в объеме слоя. Поскольку в рассматриваемых условиях (однородная деформация и постоянство потенциала на обкладках) каждая частица вещества перемещается вместе со своим значе­нием потенциала, то изменение последнего в данной точке про^ странства есть

бф = ср (г—и) — ф (г) = — и?ф = иЕ,

где Е — однородное поле внутри недеформированного слоя. Но ввиду однородности деформации имеем

и = |1, (15,5)

где z— расстояние от нижней поверхности. Поэтому вариация напряженности поля

6E = -in(El). (15,6)

Подставляя все полученные выражения в (15,4) и учитывая также, что bh = \_z = \n, получим

o_ikhn_k = ± (nD) (IE)-(in) рU+ (in) F =

 

\ 4л

Отсюда окончательно находим следующее выражение для Тензора напряжений:

0,-ъ =

Р^ др /е, г

в,* + ^Г*. (15,7)

В изотропных средах, которые здесь и рассматриваются, направ­ления Е и D совпадают. Поэтому E_iD_k = E_kD_[ и тензор (15,7), как и должно быть, симметричен '). При линейной связи D = eE имеем

F=F₀(p,T)-^e-g (15,8)

(см. (10,17)); F₀ есть свободная энергия единицы объема вещества в отсутствие поля. Согласно известному термодинамическому соотношению, производная от свободной энергии 1 г вещества по удельному объему есть давление:

fl^Ff) -'•-■>(£),--'*

х) Тот факт, что в изложенном выводе направление Е совпадает с п, не­существен, так как заранее очевидно, что может зависеть лишь от направ­ления Е, но не п.

Р

Я₀ = Я₀(р, Т) есть то давление, которое имелось бы в среде в отсутствие поля при данных значениях р и Т. Поэтому при подстановке (15,8) в (15,7) получим

— (р, T)6_lh-£[s-₉ (|)_r]'6,._{fc +} ^. (15,9)

В пустоте это выражение переходит в известный максвелловский тензор напряжений электрического поля¹).

Силы, с которыми действуют на поверхность раздела две соприкасающиеся различные среды, должны быть равны и про­тивоположны: a_ikn_k = — o'_tkn'_k, где величины со штрихом и без него относятся к двум средам. Векторы нормали п и п' имеют взаимно противоположные направления, так что можно написать

офк = °1кП_к. (15,10)

На границе двух изотропных сред равенство тангенциальных составляющих сил соблюдается тождественно. Действительно, под­ставив (15.7) в (15.10) и взяв тангенциальную компоненту, по­лучим

E_tD_n = E'_tD_n.

Но это равенство удовлетворяется уже в силу граничных усло­вий непрерывности E_t и £)„. Условие же равенства нормальных составляющих сил дает нетривиальное условие, налагаемое на разность давлений в обеих средах.

Рассмотрим, например, границу между жидкостью и атмосфе­рой (для последней можно положить е=1). Отмечая штрихом величины, относящиеся к атмосфере, и пользуясь для a_tk фор­мулой (15,9), получим

-/^,.(р.Л+£р(^)_г + Ёг(«-£?) = -Л_п.+^(^-^).

Учитывая граничные условия E_t — E'_t, D_n = еЕ_п = D'_n = E'_n, пере­пишем это равенство в виде

Р.(Р. Т)-Р_т = &(%)_т-^В-£№ + Щ). (15,11)

Это соотношение надо понимать как уравнение, определяющее плотность р жидкости вблизи ее поверхности по напряженности электрического поля в ней.

de-dp У т

£2 8л дх[

4л

*) См. примечание на стр. 49.

Определим теперь действующие в диэлектрической среде объем­ные силы. Дифференцируя согласно (15,2) выражение (15,9), получим

При учете уравнения div D = dD_k/dx_k = 0 выражение в скобках в последнем члене сводится к сумме

дхь

F ^дЕЬл.п ^дЕ> — п (^дЕ* ^дЕЛ

^кдх

обращающейся в нуль ввиду того, что rot Е = 0. Таким образом, получаем

f =

£2р

--grade (15,12)

-gradP₀(p, 7") + -^ grad

(Н. Helmholtz, 1881).

Если в диэлектрике имеются сторонние заряды с объемной плотностью р_С1, то к силе f добавится еще член Е div D/4n; по­скольку divD = 4np_CT, то этот член равен

Рсг^Е">

(15,13)

не следует, однако, думать, что этот результат самоочевиден (ср. задачу 3 § 16).

В газе, как уже было указано в § 7, можно считать разность е—1 пропорциональной его плотности. Тогда pde/dp = e — 1 и формула (15,12) принимает более простой вид:

f = -

VP₀ + Vg^rad£?- (¹⁵'¹⁴>

Формула (15,12) справедлива для сред как однородных, так и неоднородных по своему составу. В неоднородной среде е является функцией не только р и Т, но и меняющейся вдоль среды концентрации смеси. В однородной же по составу среде е есть функция только р, Т, и grade можно раскрыть как

^T-(jr).»^r+Wr

Тогда (15,12) приобретает вид:

f = -V/>.<P, Т)+{-Ч

Если и температура постоянна вдоль тела, то третий член обра­щается в нуль, а в первом можно заменить уР₀ на pV£₀ (согласно известному термодинамическому соотношению для химического по­тенциала в отсутствие поля: pd£₀ = dP₀—S₀dT) и

f =

8л \Тр)т

= — Р VC.

(15,16)

где £— химический потенциал вещества в электрическом поле (см. (10,19)).

В частности, условие механического равновесия f = 0 при постоянной температуре гласит:

C= £.-S(g)_r=const (15,17)

в согласии с общим термодинамическим условием равновесия. Обычно это условие может быть написано в еще более простом виде. Изменение плотности среды под влиянием поля само про­порционально Е'¹. Поэтому, если в отсутствие поля среда одно­родна по своей плотности, то и при наличии поля в последних двух членах в (15,15) следует полагать р = const; учет измене­ния р в формулах, предполагающих линейную связь D = еЕ, был бы превышением их точности. Тогда, приравнивая нулю f из (15,15), получим при постоянной температуре условие равновесия в виде

*'<P'^r>-ir(l)r^==Const' ^(15Л8>

отличающемся от (15,17) тем, что вместо £₀ в нем стоит Р₀/р.

В заключение этого параграфа покажем, каким образом можно вывести непосредственно выражение для силы (15,12) из формулы (14,1),— если не ставить себе целью вычисление тензора напря­жений.

Рассмотрим неограниченную неоднородную диэлектрическую среду, подвергаемую изотермической малой деформации, обра­щающейся в нуль на бесконечности. Вариация бе складывается из двух частей: 1) из изменения

е (г—и) — е (г) = — и уе,

связанного с тем, что в результате деформации в заданную точку г приходит частица вещества из точки г—и, и 2) из изменения

-(!)_rp^divu'

связанного с изменением плотности вещества в точке г: как известно (см. VII § 1), div и есть относительное изменение эле­мента объема и потому изменение плотности есть бр = — pdivu. Таким образом, вариация свободной энергии:

6<Г = 6Г₀ —J 8e^dl/ = — \ P₀divudV +

+ J£ [^и*е + (|)_г pdivu] dV (15,19)

(первый член —вариация свободной энергии в отсутствие поля). Проинтегрировав в (15,19) члены с div и по частям и сравнив

результат с выражением 8<F = — \uidV вариации свободной энер­гии через работу сил f, получим (15,12).

§ 16. Электрические силы в твердых телах

 

Диэлектрические свойства твердого тела меняются не только при изменении его плотности (как у жидкости), но и при дефор­мациях, не меняющих плотности (сдвигах). Мы рассмотрим сна­чала тела, которые в отсутствие поля изотропны. Деформация нарушает, вообще говоря, изотропию тела; в результате стано­вятся анизотропными также и его диэлектрические свойства, и скалярная диэлектрическая проницаемость е заменяется диэлект­рическим тензором в_1к.

Состояние слабо деформированного тела описывается, как известно, тензором деформации

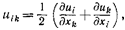где и (х, у, г) — вектор смещения точек тела. Ввиду малости этих величин в изменении компонент s_ik достаточно ограничиться лишь членами первого порядка по u_!k. Соответственно этому предста­вим диэлектрический тензор деформированного тела в виде

(16,1)

Здесь е₀—диэлектрическая проницаемость недеформированного тела, а последние два члена (с двумя скалярными постоянными а_и а₂) представляют собой наиболее общий вид тензора второго ранга, который можно составить линейным образом из компо­нент тензора u_ik.

Посмотрим теперь, в каком пункте должен быть изменен вывод, изложенный в предыдущем параграфе. Поскольку в твер­дом теле F зависит от всех компонент тензора деформации, то вместо (15,4) надо писать

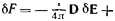
dF

Ч-ft-

 

При рассматриваемом виртуальном смещении вектор и дается формулой (15,5), так что тензор деформации

 

Подставив это в 8F и учитывая симметрию тензора u_ik (а потому и производных dF/du_lk), получим

 

4 Л. Д. Ландау, Е. М. Лифшиц

Теперь ясно, что для тензора напряжений мы получим вместо (15,7) следующее выражение¹):

 

 

Формула (16,3) применима при любой зависимости D от Е. Для непиро- (и непьезо-) электрического тела, в которомD_t=z_ikE_k, F дается формулой (13,4), и для нужных нам производных по­лучаем

■ik⁼lk~^^{aiEiEk+atE'^6ik)-

После этого везде в (16,3) полагаем e,-_fe = e₀6,-_fe и находим сле­дующую формулу для тензора напряжений:

_п __(Т(0) I ^2е0"^й1 р р Eo + g2 F2fi. /1С 4\

 

а%^] есть тензор напряжений в отсутствие электрического поля, определяющийся через модули сдвига и сжатия по обычным фор­мулам теории упругости.

х) Величина F в этой формуле, как и везде выше, есть свободная энер­гия, отнесенная к единице объема тела. В теории упругости, однако, обычно принимается несколько иное определение: термодинамические величины отно­сят к количеству вещества, заключенному в единице объема недеформирован-ного тела, которое после деформирования может занять несколько иной объем. Переход от одного определения к другому легко произвести, выражая отно­сительное изменение объема при деформации через тензор Ujk (ввиду наличия в (16,3) производной по и;к это надо сделать с точностью до членов второго порядка). В результате оба первых члена в (16,3) сведутся к одному члену вида dF/diiik, в согласии с обычной формулой теории упругости. 2) Мы увидим в § 17, что явление электрострикции в кристаллах может при определенных типах симметрии весьма существенно отличаться от электро­стрикции изотропных тел. Такие кристаллы называют пьезоэлектрическими. Здесь же будет идти речь об электрострикции в непьезоэлектрических крис­таллах.

Перейдем теперь к аналогичным вычислениям для анизотроп­ных твердых тел ²). Изменения, которые должны быть при этом внесены в изложенный выше вывод, заключаются в следующем. При виртуальной деформации слоя вещества его кристаллогра­фические оси испытывают поворот, в результате чего меняется их ориентация по отношению к электрическому полю. Ввиду анизотропии диэлектрических свойств кристалла это обстоятель­ство приводит к дополнительному изменению F, не учтенному в (16,2). При вычислении этого изменения безразлично считать, оси ли кристалла поворачиваются на некоторый угол 8<р отно­сительно поля Е или поле поворачивается относительно осей на угол —6<р; второй способ более удобен.

ЭЛЕКТРИЧЕСКИЕ СИЛЫ В ТВЕРДЫХ ТЕЛАХ

 

Таким образом, к вариации поля (15,6), рассматривавшейся нами ранее, надо прибавить изменение Е при повороте на угол — бф:

бЕ = -|п(Е1)-[б_ф.Е].

Угол бср связан с вектором смещения и при деформации посред­ством бср = ¹/₂ ^r°t и (это равенство легко получить, заметив, что при повороте тела на угол бср его точки смещаются на и = = [бср - г]). Подставив сюда и из (15,5), получим

6tp=^[vzi]=^[ni],

а затем

6Е = -1 n (Ei) +1 [Е [пЦ] = - i {n (Е1) +1 (пЕ)}. Первый член в (16,2) принимает вид

-5Г ^{D бЕ} = Ш «^nD) «^Е> + <№) ("Е)} = |f ^Е-Щ^±.

Отсюда видно, что в (16,3) произведение E_tD_k должно быть заме­нено стоящей здесь в скобках полусуммой:

°»=f «_й + £+h ^+<¹⁶-⁵)

Отметим, что полученное выражение автоматически оказывается, как и должно быть, симметричным по индексам i и /г.

Что касается диэлектрического тензора деформированного кристалла, то вместо выражения (16,1) с двумя скалярными по­стоянными мы будем иметь в общем случае выражение вида

tik = z\il + a_iklmii_lm, (16,6)

где a_iklm — постоянный тензор четвертого ранга, симметричный по парам индексов i, k и 1,т (но не симметричный по отношению к перестановке пары i,k с парой 1,т). Число отличных от нуля независимых компонент этого тензора зависит от симметрии кристалла, а именно от его кристаллического класса.

Мы не станем выписывать здесь формулы для тензора напря­жений (аналогичной (16,4)), получающейся при использовании (16,6).

Полученные формулы определяют напряжения внутри твер­дого диэлектрика. Они, однако, не нужны, если мы хотим опре­делить полную силу F или полный момент сил К, действующие на тело со стороны внешнего поля. Рассмотрим тело, погружен­ное в жидкую (или газообразную) среду и удерживаемое в ней неподвижно. Полная действующая на него сила равна интегралу

(f)a_ikn_kdf,взятому по его поверхности. В силу непрерывности

сил e_ikn_k безразлично, вычисляется ли этот интеграл по значениям a_ik из (16,4), или из формулы (15,9), относящейся к окружаю­щей тело среде. Предположим, что эта среда находится в меха­ническом и тепловом равновесии. Тогда вычисление еще более упрощается, если учесть условие равновесия (15,18). В силу этого условия часть тензора напряжений (15,9) оказывается постоян­ным вдоль среды равномерным сжимающим (или растягивающим) давлением, не дающим никакого вклада в полные действующие на тело силу F и момент сил К- Для вычисления последних можно, следовательно, писать a_ik просто в виде

^ог/*=^г(ад-т⁶'*)' ⁽¹⁶'⁷⁾

где Е — поле в жидкости, а е—-ее диэлектрическая проницаемость это выражение отличается от максвелловского тензора напряже ний электрического поля в пустоте лишь множителем е. Таким образом:

JE(nE)-l£*njdf, (16,8)

K-₄^^{[rE](nE)-i^[rnl|df. (16,9)

Отметим также, что поскольку жидкость находится в равно­весии, то в этих формулах можно производить интегрирование по любой замкнутой поверхности, охватывающей рассматриваемое тело (но, разумеется, не заключающей в себе заряженных тел, являющихся источниками поля).

К вопросу о вычислении полной силы, действующей на ди­электрик в электрическом поле (в пустоте), можно подойти и с другой точки зрения, выражая ее не через фактически сущест­вующее поле, а через то поле ©, которое создавалось бы задан­ными источниками в отсутствие диэлектрика; это есть то «внешнее поле», в которое вносится тело. При этом предполагается, что распределение зарядов, создающих поле, не меняется при внесе­нии тела в поле. Это условие может фактически не выполняться, например, если заряды распределены по поверхности протяжен­ного проводника и диэлектрик подносится на конечное расстоя­ние к нему.

При виртуальном параллельном переносе тела как целого на бесконечно малое расстояние и полная свободная энергия тела из­менится согласно (11,3) на

6Г ==* — $P6©dl/,

где

бе- = е (г+и)—© (г) = (uv) ©

есть изменение поля С? по отношению к заданной точке тела. По­скольку u= const и rot 05 = 0, имеем

р (u v) е = (pv) (и©) = и (pv) е,

так что

6<Г = —и l(Py)(SdV.

С другой стороны, 6<F = —uF, и мы приходим к следующей формуле для искомой силы *):

F= J(pv) 6-ЛУ. (16,10)

Аналогичным образом можно определить полный момент сил, действующих на тело. Не останавливаясь на соответствующих вычислениях, укажем результат:

К =S [РЩаУ+l [r-(pv)©]dv. (16,п)

В квазиоднородном поле, которое можно считать постоянным на протяжении размеров тела, формула (16,10) в первом приб­лижении дает

f = ($pdvv)<S=(^v)e, (16,12)

где —полный дипольный момент поляризованного диэлектрика, что, разумеется, можно было бы получить и прямым дифферен­цированием ¥ из (11,8). В формуле (16,11) в первом приближе­нии вообще пренебрегаем вторым членом по сравнению с первым и приходим к естественному результату:

к (16,13)

Задачи

1. Диэлектрический шар (радиуса а), находящийся во внешнем однород­ном поле СЕ, разрезан на две половины плоскостью, перпендикулярной к на­правлению поля. Определить силу притяжения между полушариями.

Решение. Представляем себе полушария разделенными бесконечно тон­кой щелью и определяем силу по формуле (16,8) (с е=1), производя в ней интегрирование по поверхности полушария, причем Е — напряженность поля в пустоте у поверхности. Согласно (8,2) поле внутри шара однородно и равно £(') — 3{ff./(2-|-e) (е—диэлектрическая проницаемость шара). Поле в щели пер­пендикулярно к поверхности и равно

*) Подчеркнем, однако, что подынтегральное выражение в этом интеграле нельзя интерпретировать как объемную плотность сил. Дело в том, что мест­ные силы в диэлектрике связаны не только с полем (?, но и с собственными внутренними полями в нем, которые, в силу закона сохранения импульса, не дают никакого вклада в полную силу, но влияют на распределение сил по объему тела.

E = DU» = ^-_e.

На внешней же поверхности шара

^Er = ^Dr^i] = © cos 0, Е_в = £</> = g sin 9,

где 0 — угол между радиус-вектором и направлением 05-

Вычисление интеграла приводит к силе притяжения, равной¹)

 

16 (е + 2)-

2. Определить изменение формы диэлектрического шара во внешнем одно-
родном электрическом поле.

Решение вполне аналогично решению задачи 4 § 5. При определении изменения формы предполагаем объем шара неизменным ²). Для упругой ча­сти свободной энергии имеем то же выражение, что и в задаче 4 § 5. Элект­рическая часть дается выражением

1^ V_ е'*> —1. ₂

2^J^~ 8л 1+п(е(*> —1) ^te

(см. (8,9)), причем диэлектрическая проницаемость вдоль оси х согласно (16,1)

= е₀ + а₁